Оценка ценных бумаг и принятие решений по финансовым операциям
В данном параграфе будут рассмотрены теоретические и методические основы оценки вложения средств в ценные бумагу. Связано это с тем, что данные вопросы в отношении именно этих видов финансовых инвестиций имеют наибольшую практическую востребованность.
Предприятия вкладывают деньги в ценные бумаги в основном с целью получения доходов и сохранения капитала от инфляции. Однако чтобы сформировать эффективный и надежный инвестиционный портфель ценных бумаг, необходимо знать характеристики и назначения различных видов ценных бумаг, правила их выпуска, обращения, а главное методы оценки такого рода инвестиций.
Ценная бумага – это денежный документ, который удостоверяет имущественное право или отношение займа владельца документа к лицу, выпустившему такой документ (акция, облигация, ГКО и т.д.).
Совокупность всех ценных бумаг, принадлежащих инвестору, называют портфелем ценных бумаг. При формировании портфеля ценных бумаг владелец должен обеспечить:
‒ безопасность вложения капитала в ценные бумаги;
‒ заданную доходность вложений;
‒ рост капитала и его ликвидность.
При этом следует помнить, что основным принципом оптимизации портфеля ценных бумаг является принцип диверсификации финансовых вложений, то есть распределение вложений между множеством разных по инвестиционным качествам ценных бумаг с целью снижения риска общих потерь и повышения совокупной доходности.
Согласно фундаменталисткой теории, любая ценная бумага имеет внутренне присущую ей ценность, количественно оцениваемую как дисконтированную стоимость будущих поступлений, генерируемых этой бумагой (т.е. нужно двигаться от будущего к настоящему). Проблема здесь состоит в точности определения этих поступлений, что зависит от ряда обстоятельств: анализ ситуации на рынке, инвестиционной и дивидендной политики компании, инвестиционных ее возможностей и т.п.
Текущая внутренняя стоимость (P) любой ценной бумаги в общем виде может быть рассчитана по формуле (13):
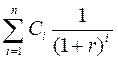
где С – денежные поступления по ценной бумаге.
Подставляя в эту формулу значения предполагаемых поступлений, доходности и продолжительности периода прогнозирования, можно рассчитать текущую внутреннюю стоимость любого финансового актива. Именно такого подхода чаще всего и придерживаются потенциальные инвесторы. В частности, «приемлемая норма дохода может устанавливаться инвестором следующим образом:
‒ в размере процентной ставки по банковским депозитам;
‒ исходя из процента, выплачиваемого банком вкладчику за хранение его средств, и надбавки за риск инвестирования в данный финансовый актив;
‒ исходя из процента, выплачиваемого по правительственным облигациям (в странах с некризисной экономикой), и надбавки за риск»[14].
Применение данного подхода рассмотрим применительно к оценке основных видов финансовых активов: облигаций и акций.
Облигации– это долговые ценные бумаги с фиксированным процентом дохода (в классическом варианте долгосрочные долговые обязательства корпораций, федерального правительства, местных органов власти). Облигации имеют нарицательную (или номинальную), выкупную и рыночную цену.
Номинальная цена (N) напечатана на самой облигации и используется в качестве базы для начисления процентов.
Выкупная цена – это цена, по которой производится выкуп облигации эмитентом по истечении срока займа; она может совпадать с нарицательной стоимостью и определяться условиями займа.
Рыночная (курсовая) цена облигации определяется конъюнктурой рынка.
Значение рыночной цены облигации в процентах к номиналу называется курсом облигации.
Для исчисления текущей стоимости облигации (Р) необходимо рассчитать суммарную текущую стоимость данных денежных поступлений. Сделать это можно без применения (формула (19) и с применением (формула (20) дисконтирующих множителей.
Р = 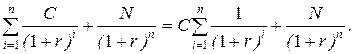 (19)
(19)
При расчете текущей стоимости облигации с применением дисконтирующих множителей следует иметь ввиду, что первая часть формулы (19) представляет собой аннуитет (денежный поток с равными поступлениями), поэтому для нее используется дисконтирующий множитель FM4(r;n). Вторая часть формулы – однократное поступление, поэтому используем дисконтирующий множитель FM2(r;n).
Р = С × FM4(r;n) + N × FM2(r;n) (20)
Исчислить текущую стоимость бессрочной облигации при известной величине выплачиваемого по ней годового дохода и рыночной доходности возможно на основе формулы бессрочного аннуитета:
Р = С : r (21)
где: Р – настоящая стоимость будущего дохода облигаций;
r – рыночная доходность облигации;
С – величина годового дохода, выплачиваемого по облигации.
Расчет текущей стоимости облигации с внутригодовым начислением процентов осуществляется по формуле:
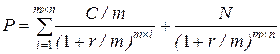 =
=
С/m × FM4 (r/m; m×n) + N×FM2 (r/m; m×n), (22)
где С – годовой процентный доход;
m – число внутригодовых начислений процентов;
n – число лет обращения облигации;
r – требуемая норма прибыли (коэффициент дисконтирования);
N – номинал облигации.
Акции представляют собой долевые ценные бумаги, удостоверяющие право ее владельца на долю в собственности эмитента, на получение дохода от его деятельности и на участие в управлении им. Акции являются корпоративными ценные бумаги и выпускаются только негосударственными предприятиями и организациями. Они не имеют установленных сроков обращения и, как правило, приносят изменяющийся (плавающий, не фиксированный доход).
Различают несколько видов цены акции: номинальная, эмиссионная, балансовая, ликвидационная, курсовая.
Номинальная цена акции – это цена, указанная на бланке акции.
Эмиссионная цена представляет собой цену, по которой акция эмитируется, то есть продается на первичном рынке.
Ликвидационная цена может быть определена лишь в момент ликвидации общества.
Курсовая (рыночная, текущая) цена котировки акций на вторичном рынке ценных бумаг.
Существует множество разновидностей акций. Наиболее типичными являются привилегированные и обыкновенные акции.
Привилегированные акции, как и бессрочные облигации, генерируют гарантированный доход и право на получение ее стоимости при ликвидации компании до выплат по обыкновенным акциям.
Обыкновенные акции предоставляют право собственности в корпорации и в отличии от привилегированных дают право голоса на собрании акционеров.
Инвестиционная привлекательность акций состоит в том, что риск возможных потерь денежных вложений как бы компенсируется возможность получения более высокого дохода. Для оценки этой ситуации достаточно сравнить размеры дивиденда на акцию со средней ставкой процента по депозитному счету в банке. При этом приобретение акции будет целесообразно в том случае, если ставка дивиденда выше процентной ставки по депозиту.
Для устранения неопределенности при инвестировании средств в акции теорией и практикой инвестиционного анализа выработан такой подход к оценке их стоимости, как метод капитализации чистой прибыли, являющийся наиболее простым. В формализованном виде сущность метода представлена формулой (21), в которой в данном случае: Р – настоящая стоимость будущего дохода (чистой прибыли на акцию); С – ожидаемая (средняя за период) будущая чистая прибыль на акцию; s – норма капитализации или норма риска.
В практике инвестиционного анализа встречаются следующие аналитические задачи оценки финансовых вложений в форме приобретения акций:
1. Оценка значений ожидаемой общей доходности обыкновенных акций с равномерно возрастающими дивидендами, для чего можно воспользоваться формулой (23), полученной на основе модели Гордона:
Р = 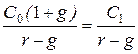 , (23)
, (23)
где С0 - последний выплаченный дивиденд;
С1 – прогнозируемый дивиденд за текущий период;
r – требуемая норма прибыли (коэффициент дисконтирования) (в доле единицы);
g – темп прироста дивидендов (в доле единицы).
2. Обоснование выбора того или иного проекта финансовых инвестиций. В данном случае задача сводится к выбору наименее рискового проекта, для чего необходимо рассчитать: среднеожидаемую доходность (формула (24)), среднеквадратическое (стандартное) отклонение (формула (25)) и коэффициент вариации каждого финансового актива (формула (26)). Два последних показателя характеризуют количественный риск финансовых вложений.
Среднеожидаемая доходность (ko):
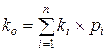 , (24)
, (24)
где ki – возможная доходность i-го актива;
рi – вероятность проявления.
Среднеквадратическое (стандартное) отклонение (характеризует абсолютный разброс данных о доходности ценных бумаг вокруг среднего (ожидаемого) значения) (s):
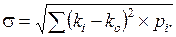 (25)
(25)
Коэффициент вариации (показывает, на сколько процентов отдельные значения доходности в среднем отклоняются от ожидаемой величины) (V):
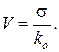 (26)
(26)
Чем выше разброс возможной доходности вокруг среднего значения (выше коэффициент вариации), тем вложения в финансовый актив считаются более рискованными.
3. Оценка доходности акций (в т.ч. портфеля акций). Аналитические расчеты в рамках решения данной задачи осуществляются на основе следующих показателей:
Бета-коэффициент (b) – индекс доходности данного актива по отношению к доходности рынка ценных бумаг в целом. Модель оценки доходности финансовых активов (Capital Asset Pricing Model, CAPM):
Ko = Kf + b (Km - Kf), (27)
где Ko – ожидаемая доходность акций данной компании;
Kf - доходность безрисковых ценных бумаг (за рубежом таковыми, как правило, считаются государственные ценные бумаги);
Km - средняя доходность на рынке;
b - бета-коэффициент для данной компании.
Если акции конкретной компании имеют бета-коэффициент:
‒ равный 1,0, то их ожидаемая доходность равна среднерыночной;
‒ выше 1,0, то их ожидаемая доходность выше среднерыночной;
‒ ниже 1,0, то их ожидаемая доходность ниже среднерыночной;
‒ равный 0, то их ожидаемая доходность равна доходности безрисковых ценных бумаг.
Графически зависимость между бета-коэффициентом и доходностью представляет собой прямую, проходящую через две точки:
‒ (b=0; Ko=доходности безрисковых ценных бумаг);
‒ (b=1; Ko=среднерыночной доходности).
Бета-коэффициент портфеля (bп) рассчитывается по формуле средневзвешенной:
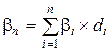 , (28)
, (28)
где bi – бета-коэффициент i-го актива;
di – доля i-го актива в портфеле.
Ожидаемая доходность портфеля (Коп) может быть исчислена двумя способами:
1) на основании модели CAPM, куда подставляется бета-коэффициент портфеля;
2) по формуле средневзвешенной:
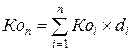 , (29)
, (29)
где Коi – ожидаемая доходность i-го актива;
di – доля i-го актива в портфеле.
Ожидаемая доходность портфеля сравнивается со средней рыночной, что составляет основу формирования финансово-экономической оценки ситуации (положительно, если первая превышает вторую).
Практические аспекты применения вышерассмотренных формул раскрыты в п.2.2 учебного пособия.
Дата добавления: 2016-02-02; просмотров: 1373;
