Финансовых вычислений
Базовая концепция инвестиционного анализа и основы
финансовых вычислений
Процесс анализа эффективности вложений средств как в денежные, так и в реальные активы базируется на фундаментальной концепции временной ценности денег.
Одной из основных причин возникновения методов оценки инвестиционных проектов является неодинаковая ценность денежных средств во времени. Практически это означает следующее: рубль сегодняшний считается нетождественным рублю через год. Причина разного отношения к одной и той же денежной сумме состоит в том, что рубль, вложенный в те или иные коммерческие операции, способен через год превратиться в большую сумму за счет полученного дохода. Данный принцип порождает концепцию оценки стоимости денег во времени:стоимость денег с течением времени изменяется с учетом нормы прибыльности на денежном рынке и рынке ценных бумаг (в качестве нормы прибыльности может выступать норма ссудного процента или норма выплаты дивидендов по обыкновенным и привилегированным акциям).
Данное положение является аксиомой финансовых операций и предопределяет весь процесс экономического обоснования и оценки инвестиционных проектов. Учитывая, что инвестирование представляет собой обычно длительный процесс, в инвестиционной практике обычно приходится сравнивать стоимость денег в начале их инвестирования со стоимостью денег при их возврате в виде будущей прибыли.
В финансовом менеджменте фактор времени учитывается с помощью методов наращения и дисконтирования, в основу которых положена техника процентных вычислений. С помощью данных методов осуществляется приведение денежных сумм, относящихся к различным временным периодам, к требуемому моменту времени в настоящем или будущем.
В процессе сравнения стоимости денежных средств при их вложении и возврате принято использовать два основных понятия: настоящая (современная) стоимость денег и будущая стоимость денег.
Будущая стоимость денег (F (future)) представляет собой ту сумму, в которую превратятся инвестированные в настоящий момент денежные средства через определенный период времени с учетом определенной процентной ставки (т.е. это возвращаемая сумма с процентами).
Определение будущей стоимости денег связано с процессомнаращения (compounding) начальной стоимости. Экономический смысл метода наращения: определяется величина, которая будет или может быть получена из некоторой первоначальной (текущей) суммы в результате проведения операции.
Итак, наращение – это поэтапное увеличение вложенной суммы путем присоединения к первоначальному ее размеру суммы процентных платежей. То есть данный метод позволяет определить будущую величину (F) текущей суммы инвестиций через некоторый промежуток времени, исходя из заданной процентной ставки r.
В узком смысле процентная ставка r (interest rate) представляет собой цену, уплачиваемую за использование заемных денежных средств, и показывает степень интенсивности изменения стоимости денег во времени. В финансовом менеджменте ее часто используют не только как инструмент наращения стоимости денежных средств, но и как измеритель степени доходности инвестиционных операций, исчисляемый отношением получаемой прибыли к величине вложенных средств (в долях единицы либо в %).
Процентная ставка - это относительная величина процента (дохода, который является абсолютной величиной).Ставка процента (r) определяется по формуле:
 , (1)
, (1)
где: P – современная или первоначальная сумма вложений;
F – будущая сумма, т.е.возвращаемая сумма с процентами;
(F – Р) – сумма процентов (доход).
Настоящая (современная, текущая, первоначальная) стоимость денег (P (present)) представляет собой сумму будущих денежных поступлений, приведенных к настоящему моменту времени с учетом определенной процентной ставки. Определение настоящей стоимости денег связано с процессом дисконтирования(discounting) будущей стоимости, который (процесс) представляет собой операцию, обратную наращению.
Дисконтирование представляет собой процесс нахождения первоначальной величины на заданный момент времени по ее известному или предполагаемому значению в будущем, исходя из заданной процентной ставки. Экономический смысл дисконтирования: величина текущей суммы инвестиций Р, найденная в процессе дисконтирования, показывает современное (с позиции текущего момента времени) значение будущей величины F.
Используемую при этом процентную ставку называют ставкой дисконтирования (ставка дисконта, нормой дисконта, учетная ставка) (d), величина которой определяется по формуле:
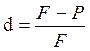 , (2)
, (2)
где: (F – P) – сумма дисконта (доход).
Сравнивая формулы (1) и (2), можно заметить, что сумма процентов и величина дисконта (числитель формул) определяются одинаково – как разница между будущей и современной стоимостями. Однако, смысл, вкладываемый в эти величины, имеет разную трактовку: «в первом случае речь идет о приросте текущей стоимости, своего рода «наценке», то во втором определяется снижение будущей стоимости, «скидка» с ее величины (diskont в переводе с немецкого означает «скидка»)»[12].
В зависимости от условий проведения финансовых операций как наращение, так и дисконтирование могут осуществляться с применением простых или сложных процентов. При начислении простых процентов наращение первоначальной суммы происходит в арифметической прогрессии, а при начислении сложных процентов – в геометрической.
Рассмотрим подробно операции с простыми процентами.
Простая процентная ставка – это такая ставка, при которой процент начисляется на первоначально вложенную сумму средств. Таким образом, базой для исчисления процентов в этом случае служит первоначальная (исходная сумма сделки), которая ежегодно увеличивается на величину (P×r). Простые процентные ставки используются в основном в краткосрочных финансовых операциях, срок проведения которых меньше года.
В общем случае наращение и дисконтирование по ставке простых процентов осуществляются по формулам, приведенным в табл 4.
Таблица 4
Формулы проведения финансовых вычислений по ставке простых
процентов (при финансовых операциях с целым числом лет)
| Наращение | Дисконтирование |
| F = P × (1+r×n)(3) | P = F:(1 + r×n)(4) |
| n – число периодов (целое число лет финансовой операции), r – ставка процентов |
Как правило, процентные ставки устанавливаются в годовом исчислении, поэтому они называются годовыми. Особенностью простых процентов является то, что частота процессов наращения в течение года не влияет на результат. Иначе: например, нет никакой разницы начислять 20% годовых 1 раз в год или начислить 2 раза по 10% годовых. Простая ставка 20% годовых при одном начислении в году называется эквивалентной простой ставке 10% годовых при начислении 1 раз в полгода.
Данная ситуация связана с тем, что процесс наращения по простой процентной ставке представляет собой арифметическую прогрессию с первым членом a1 = P и величиной (P× r):
P, P + (P × r), P + 2 × (P × r), P + 3 × (P × r), …, P + (k – 1) × (P × r)
Наращенная сумма F в данном случае – это последний k-й член этой прогрессии, т.е.:
F = ak = P + n × P × r,
где: срок финансовой операции n равен (k – 1).
Поэтому, если увеличить количество раз начисления процентов (n)и одновременно пропорционально уменьшить ставку процентов (r), то величина каждого члена прогрессии, в том числе и последнего, останется неизменной.
Следует помнить, что продолжительность финансовой операции, связанной с начислением процентов (n), не всегда составляет год или целое число лет. Напротив, простые проценты чаще всего используются при краткосрочных (длительностью менее года) операциях. В этом случае возникает проблема определения длительности ссуды и продолжительности года в днях.
Обозначив продолжительность года в днях буквой Т (этот показатель называется временная база), а количество дней финансовой операции t, то использованное в формулах (3) и (4) обозначение количества полных лет n можно будет выразить как t/Т. Подставляя это выражение в формулы (3) и (4), получаем расчетные формулы, приведенные в таблице 5.
Таблица 5
Формулы проведения финансовых вычислений по ставке простых
процентов (при финансовых операциях с внутригодовыми начислениями)
| Наращение | Дисконтирование |
| F = P × (1+r × t/Т)(5) | P = F:(1 + r× t/Т)(6) |
| Т– продолжительность года в днях, t – количество дней финансовой операции |
Основной областью применения простых процентной и учетной ставок являются краткосрочные финансовые операции, длительность которых менее 1 года. Вычисления с простыми ставками не учитывают возможность реинвестирования начисленных процентов, потому что наращение и дисконтирование производятся относительно неизменной исходной суммы P или F. В отличие от них сложные ставки процентов учитывают возможность реинвестирования процентов, так как в этом случае наращение производится по формуле не арифметической, а геометрической прогрессии
Сложная процентная ставка– это такая ставка, при которой процент начисляется на постоянно нарастающую базу с учетом процентов, начисленных в предыдущие периоды («процент на проценты»). Итак, их сущность заключается в следующем: очередной годовой доход исчисляется не от исходной величины P, а с общей суммы, включающей также и ранее начисленные и не востребованные инвестором проценты, т.е. проценты присоединяются к сумме вклада (происходит капитализация процентов).
Сложные проценты применяются при долгосрочных финансовых вложениях со сроком более одного года. Однако они могут применяться и в краткосрочных финансовых операциях, но если это объективно необходимо. Например, при высоком уровне инфляции или риска.
В общем случае наращение и дисконтирование по ставке сложных процентов при проведении финансовых операций с целым числом лет осуществляются по формулам, приведенным в табл 6.
Таблица 6
Формулы проведения финансовых вычислений по ставке сложных
процентов (при финансовых операциях с целым числом лет)
| Наращение | Дисконтирование |
| F = P × (1+r)n (7) | P = F : (1+r)n (8) |
| (1+r)n и (1:(1+r)n) – факторные множители, которые для удобства обозначаются иногда FM1 и FM2 соответственно (их числовые значения берутся из специальных таблиц, приведенных в приложении А). |
Экономический смысл факторного мультиплицирующего множителя FM1(r,n) состоит в следующем: он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через n периодов при заданной процентной ставке r.
Экономический смысл факторного дисконтирующего множителя FM2(r,n) состоит в следующем: он показывает «сегодняшнюю» цену одной денежной единицы будущего, т.е. чему с точки зрения текущего момента равна одна денежная единица (например, один рубль, один доллар и т.д.), циркулирующая в сфере бизнеса n периодов спустя от момента расчета, при заданных процентной ставке (доходности) r (иногда учитывают также частоту начисления процента).
Важной особенностью сложных процентов является зависимость конечного результата от количества начислений в течение года. Здесь опять сказывается влияние реинвестирования начисленных процентов: база начисления возрастает с каждым новым начислением, а не остается неизменной, как в случае простых процентов.
Например, если начислять 20% годовых 1 раз в год, то первоначальная сумма в 10 тыс. рублей возрастет к концу года до 12,00 тыс. рублей (10 × (1+ 0,2)). Если же начислять по 10% каждые полгода, то будущая стоимость составит 12,10 тыс. рублей (10 × (1 + 0,1) × (1 + 0,1)), при поквартальном начислении по 5% она возрастет до 12,16 тыс. рублей. Другими словами, по мере увеличения числа начислений (m) и продолжительности операции эта разница будет очень сильно увеличиваться. Если разделить сумму начисленных процентов при ежеквартальном наращении на первоначальную сумму, то получится 21,6% ((12,16 – 10,00) : 10 × 100), а не 20%. В этой связи, сложная ставка 20% при однократном наращении и 20% при поквартальном наращении приводят к различным результатам, то есть они не являются эквивалентными. Цифра 20% отражает уже не действительную (эффективную), а номинальную ставку. Эффективной процентной ставкой является значение 21,6%.
Номинальная процентная ставка – это исходная годовая ставка для начисления процента.
Эффективная процентная ставка – это годовой процент прироста первоначальной суммы вложений с внутригодовыми начислениями доходов.
Формулы операций наращения и дисконтирования по сложным процентам с внутригодовыми начислениями приведены в табл.7
Таблица 7
Формулы проведения финансовых вычислений по ставке сложных
процентов (при финансовых операциях с внутригодовыми начислениями)
| Наращение | Дисконтирование |
| F = P × (1+r/m)nm (9) | P = F : (1+ r/m)nm (10) |
| m – число начислений в году |
Основные правила процентных вычислений, рассмотренные выше верны как для разовых платежей, так и для их совокупности. Оценка денежного потока F1, F2, ….., Fn, генерируемого в течение ряда временных периодов в результате реализации какого-либо проекта или функционирования того или иного вида активов - один из основных элементов инвестиционного анализа.
Элементы потока F, могут быть либо независимыми, либо связанными между собой определенным алгоритмом. Помимо того, что временные периоды чаще всего предполагаются равными, еще предполагается, что элементы денежного потока являются однонаправленными, т.е. нет чередования оттоков и притоков денежных средств. Также считается, что генерируемые в рамках одного временного периода поступления имеют место либо в его начале, либо в его конце, т.е. они не распределены внутри периода, а сконцентрированы на одной из его границ. В первом случае поток называется потоком пренумерандо, или авансовым, во втором - потоком постнумерандо. Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.
На рис.3. приведены примеры наглядного графического представления потоков пренумерандо и постнумерандо для периода в шесть лет.
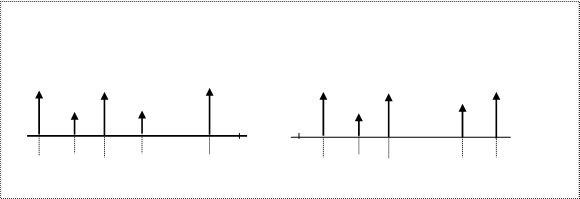
А. Поток пренумерандо Б. Поток постнумерандо
F1 F2 F3 F4 … Fn F1 F2 F3 … Fn-1 Fn
0 1 2 3 … (n-1) n 0 1 2 3 … (n-1) n
Рисунок 3 - Графическое представление денежных потоков (F)
пренумерандо и постнумерандо[13]
Оценка денежного потока может выполняться в рамках решения двух задач:
1) прямой, т.е. проводится оценка с точки зрения будущего (реализуется схема наращения);
2) обратной, т.е. проводится оценка с точки зрения настоящего (реализуется схема дисконтирования).
Прямая задача предполагает суммарную оценку наращенного денежного потока, т.е. в ее основе лежит будущая стоимость. В частности, если денежный поток представляет собой регулярные начисления процентов на вложенный капитал (Р) по схеме сложных процентов, то в основе суммарной оценки наращенного денежного потока лежит формула (7).
Обратная задача, которая является основной при оценке инвестиционных проектов, предполагает суммарную оценку дисконтированного (приведенного) денежного потока. Поскольку отдельные элементы денежного потока генерируются в различные временные интервалы, а деньги имеют временную ценность, непосредственное их суммирование невозможно. Приведение денежного потока к одному моменту времени осуществляется при помощи формулы (8). Основной результат расчета - определение общей величины приведенного денежного потока, но используемые при этом расчетные формулы различны в зависимости от вида денежного потока - постнумерандо или пренумерандо.
Формулы для определения стоимости денежного потока пренумерандо и постнумерандо при операциях наращения и дисконтирования приведены в табл.8.
Таблица 8
Формулы расчета определения стоимости денежного потока в разрезе его видов (пренумерандо и постнумерандо) при операциях
наращения и дисконтирования
| Виды денежных потоков | Наращение | Дисконтирование |
| Постнумерандо | Fpst= 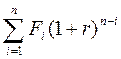 (11) (11)
| Pprs = 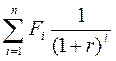 (13) (13)
|
| Пренумерандо | Fpre = Fpst×(1+r) (12) | Ppre= Pprs ×(1+r) (14) |
| Fpst - будущая стоимость исходного денежного потока постнумерандо;Fpre - будущая стоимость исходного денежного потока пренумерандо; Ppst - приведенная стоимость денежного потока постнумерандо;Ppre - приведенная стоимость денежного потока пренумерандо; i – отдельный денежный платеж |
В инвестиционном анализе для обозначения денежных потоков (ƩFi) в наиболее общем смысле используется термин рента. Каждый отдельный рентный платеж (Fn) называют членом ренты. Частным случаем ренты является финансовая рента или аннуитет.
Аннуитет (А) – это такой поток платежей, все члены которого равны друг другу, так же как и интервалы времени между ними (иначе - это денежный поток, состоящий из ежегодно одинаковых денежных сумм, т.е. в этом случае ƩFi = А).
Часто аннуитетом называют финансовый актив, приносящий фиксированный доход ежегодно в течение ряда лет. В буквальном переводе «аннуитет» предполагает, что платежи происходят с интервалом в один год, однако встречаются потоки с иной периодичностью выплат. Очевидно, что рента – это более широкое понятие, чем аннуитет, так как существует множество денежных потоков, члены которых не равны друг другу или распределены неравномерно.
Для оценки будущей и приведенной стоимости аннуитета можно пользоваться вышеприведенными в табл.8 формулами. Однако из-за специфики аннуитетов – равенство денежных поступлений – эти формулы могут быть существенно упрощены.
В частности, для решения прямой задачи (наращение) оценки срочных аннуитетов постнумерандо и пренумерандо при заданных величинах регулярного поступления (А) и процентной ставке (r) можно воспользоваться формулами (15) и (16), приведенными в табл. 9.
Для решения обратной задачи (дисконтирование) оценки срочных аннуитетов постнумерандо и пренумерандо, являющейся основной при анализе инвестиционных проектов, денежные притоки которых имеют вид аннуитетных поступлений, можно воспользоваться формулами (17) и (18), представленными в табл. 9.
Таблица 9
Формулы оценки срочных аннуитетов при операциях
наращения и дисконтирования в разрезе видов денежных потоков
(пренумерандо и постнумерандо)
| Виды денежных потоков | Наращение | Дисконтирование |
| Постнумерандо | FpstА= A× 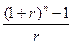 =
A× FM3 (15) =
A× FM3 (15)
| Pprs А = 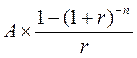 =
А× FM4 (17) =
А× FM4 (17)
|
| Пренумерандо | FpreА= FpstА×(1+r)= А× FM3 ×(1+r) (16) | PpreА = Pprs ×(1+r) = А× FM4×(1+r) (18) |
FM3 – факторный (мультиплицирующий) множитель для аннуитета:
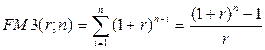 FM4 – дисконтирующий множитель для аннуитета:
FM4 – дисконтирующий множитель для аннуитета:
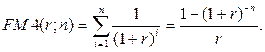
|
Экономический смысл мультиплицирующего множителя для аннуитета FM3(r,n) заключается в следующем: он показывает, чему равна с точки зрения текущего момента величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что денежные суммы лишь начисляются, а изъять их можно по окончании срока действия аннуитета.
Экономический смысл дисконтирующего множителя для аннуитета FM4(r,n) заключается в следующем: он показывает, чему равна с точки зрения текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы (например, один рубль), продолжающегося n равных периодов с заданной процентной ставкой r.
Значения этого множителей FM3(r,n) и FM4(r,n) также как и множителей FM1(r,n) и FM2(r,n), табулированы (их числовые значения приведены в приложении А).
Таким образом, финансовые вычисления, базирующиеся на понятии временной стоимости денег – это один из краеугольных элементов финансового менеджмента и используются в различных его разделах. Наиболее интенсивно они применяются:
а) в операциях на рынке ценных бумаг,
б) в ссудо-заемных операциях;
в) в оценке бизнеса;
г) для оценки инвестиционных проектов, связанных с вложением средств в реальные инвестиции.
Дата добавления: 2016-02-02; просмотров: 4278;
