Оценка ценных бумаг и принятие решений по финансовым инвестициям. 1. В общем виде текущая рыночная стоимость (Vm) любой ценной бумаги может быть рассчитана по формуле (CFi - ожидаемый поток в i-том периоде; r - приемлемая

1. В общем виде текущая рыночная стоимость (V_m) любой ценной бумаги может быть рассчитана по формуле (CF_i - ожидаемый поток в i-том периоде; r - приемлемая норма дохода):

а)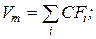

б)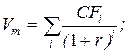

в)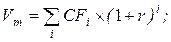

г)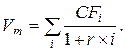

2. При оценке целесообразности приобретения ценных бумаг:

а) их текущая стоимость сравнивается с фактически сложившейся на рынке;

б) сравниваются значения банковской процентной ставки и ежегодный доход по ценной бумаге в процентном выражении к номиналу;

в) ежегодный доход по ценной бумаге в процентном выражении к номиналу сравнивается со средней нормой доходности на рынке;

г) сравнивается номинал ценной бумаги и ее рыночная стоимость.

3. Модель Гордона используется для:

а) оценки купонных облигаций;

б) оценки бескупонных облигаций;

в) оценки акций с постоянным размером дивиденда;

г) оценки акций с постоянным темпом прироста дивидендов.

4. Модель Гордона имеет вид (С_о – последний выплаченный дивиденд; g – темп прироста дивиденда; С₁ - планируемый дивиденд за текущий год):

а)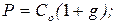

б)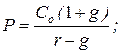

в)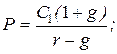

г)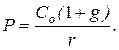

5. Для оценки текущей стоимости облигации с ежегодным начислением процентов и погашением через n лет используют формулу (С - ежегодный процентный доход; N - номинал облигации):

а)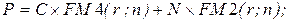

б)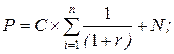

в)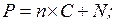

г)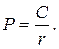

6. Если рыночная норма дохода превосходит фиксированную купонную (процентную) ставку, облигация продается:

а) с премией, т.е. по цене выше номинала;

б) со скидкой, т.е. по цене ниже номинала;

в) по цене, равной номиналу;

г) цена продажи не зависит от этого состояния.

7. С ростом рыночной нормы дохода текущая стоимость ценной бумаги:

а) убывает;

б) возрастает;

в) не меняется.

8. Текущая стоимость облигации с внутригодовым начислением процентов и погашением номинала (N) через n лет (m – число начислений процентов в году; С – сумма процентов, исчисленная из годовой процентной ставки):

а)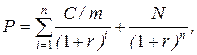

б)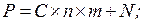

в)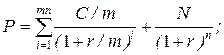

г)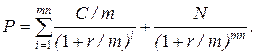

9. Бета-коэффициент отражает:

а) степень изменения дивидендной доходности акции от изменения доходности рынка в целом;

б) степень изменения доходности отдельного фондового инструмента от изменения доходности рынка в целом;

в) степень изменения доходности финансовых вложений организации от изменения доходности безрисковых ценных бумаг;

г) среднерыночный риск вложений в фондовые инструменты.