Корреляционный анализ. 3.2.1 Обзор характеристик «тесноты» связи

3.2.1 Обзор характеристик «тесноты» связи

Выделяют три разновидности характеристик степени «тесноты» статистической связи между величинами по мере увеличения их наглядности (рис. 2.1).

1. Табличные (так называемые «таблицы сопряжённости», «корреляционные матрицы» или «корреляционные таблицы»). Как показано в табл. 2.1, в данном случае заголовки граф и столбцов («сказуемое таблицы») представляют собой последовательные значения исследуемых переменных. (В первом столбце и первой строке корреляцион­ной таблицы могут указываться сере­дины или границы интервалов изменения случайных величин.) В клетках на пересечениях граф и столбцов («подлежащее таблицы») наносятся соответствующие частоты. Такая таблица реализуется в рамках программы MS EXCEL и может наглядно представлять связь двух переменных. Например, по табл. 2.1 можно обнаружить, что в некотором процессе черновой обработки резанием с увеличением подачи увеличивается шероховатость поверхности.

Рис. 2.1. Предлагаемая схема всевозможных характеристик «тесноты» связи

Таблица 2.1. Корреляционная матрица x (характеристика подачи при механической обработке) и y (характеристика шероховатости Rz)

2. Графические, когда по осям координат откладываются интервалы изменения пе­ременных и наносится координатная сетка. Каждую пару пере­менных из данной выборки в этом «поле корреляции» изображают точкой. Часто точки (x_i, y_i) связывают «линией тренда», являющейся по сути графическим представлением уравнения регрессии (рис. 2.2). По близости точек к этой линии на «корреляционном графике» можно наглядно судить о степени «тесноты» связи.

В главе 5 показано, что графические опции MS EXCEL позволяют не только строить «линии тренда» любой формы, но и автоматически определять (рассчитывать) соответствующие им уравнения регрессии, а также объективно аналитически оценивать степень точности описания ими расположения точек (x_i, y_i).

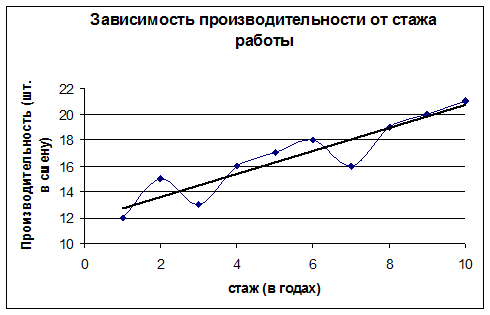
Рис. 2.2. Пример корреляционного графика с прямой линией тренда

3. Аналитические характеристики «тесноты» связи на представленной схеме (см. рис. 2.1) отражают лишь оценки классического корреляционного анализа, предполагающего нормальное распределение рассматриваемых случайных величин. Следует знать о многочисленных имеющихся методах непараметрического корреляционного анализа:

- с помощью порядковых статистик;

- ранговая корреляция (как достаточно часто используемая рассмотрена ниже, см. § 3.2.4);

- точечно-бисериальная корреляция;

- статистическая оценка связи между качественными признаками по таблицам сопряжённости.

Наиболее часто используемые аналитические характеристики «тесноты» связи (см. рис. 2.1) делятся на следующие виды:

- коэффициенты ковариации;

- коэффициенты корреляции (для парной, множественной и частной корреляции);

- корреляционное отношение (для криволинейной связи случайных величин);

- коэффициенты детерминации;

- Q - коэффициенты (редко применяются в технике).

3.2.2. Формулы расчёта основных характеристик связи

Коэффициент ковариации(ковариация) определяется как среднее произведений отклонений от выборочных средних значени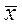й и 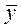для каждой пары из n точек данных:

cov (x y) = 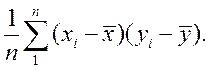(2.1)

Формула (2.1) показывает, что ковариация значительна, когда большое отклонение 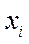от 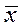сочетается с большим отклонением 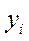от .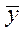

Значения коэффициента корреляции колеблются от -1 до +1. Знак плюс указывает на "положительную корреляциционную связь", а знак минус - на отрицатель­ную. Коэффициент корреляции, равный ±1, указывает на функци­ональную зависимость между переменными.

Следует подчеркнуть, что обращение в нуль ковариации переменных X и Y является не достаточным, а только необходимым условием для суждения об их независимости. С другой стороны, ненулевое значение ковариации говорит о некоторой связи случайных величин, но не позволяет судить о степени тесноты и достоверности этой связи. Из формулы (2.1) можно сделать заключение, что при переходе к другой единице измерения (например, от метров к сантиметрам) значение ковариации также изменяется.

Коэффициент корреляции Пирсона (обозначается r или ρ) называется также «коэффициентом линейной корреляции», так как измеряет степень линейной связи между переменными. Иначе говоря, он определяет степень пропорциональности друг другу значений двух переменных коэффициент корреляции Пирсона можно рассчитать по формулам:

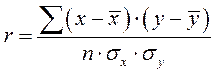(2.2)

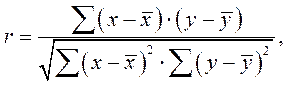или (2.3)

где σ_x (S_x), σ_y (S_y) - среднеквадратические отклонения генеральных совокупностей (или выборок) переменных X и Y.

Анализ формул (2.2) - (2.3) позволяет сделать заключение, что коэффициент корреляции - величина безразмерная (в отличие от коэффициента ковариации). Сравнение формул (2.1) и (2.2) показывает, что коэффициент Пирсона равен ковариации двух переменных, делённой на произведение их стандартных отклонений.

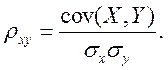(2.4)

Коэффициент корреляции, как и коэффициент ковариации, характеризует степень линейной зависимости случайных величин Х и Y, проявляющейся в том, что при возрастании одной случайной величины другая проявляет тенденцию также возрастать (или, наоборот, убывать). В первом случае (r_xy > 0) случайные величины связаны «положительной корреляцией», во втором случае (r_xy < 0) наблюдается «отрицательная корреляция».

Множественный коэффициент детерминации (R²), представ­ляющий собой множественный коэффициент корреляции (см. рис. 2.1) в квад­рате, характеризует, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в мно­гофакторную регрессионную модель. Чем больше R², тем больше результат (отклик) зависит от действующих факторов. Чем меньше R², тем больше действие случайных и неучтённых факторов. Таким образом, R² характеризует, насколько хорошо модель описывает («аппроксимирует») экспериментальные точки.

Важно понять механизм "работы" приведённых формул: чем больше совместное отклонение x и y от их средних значений, тем больше |r| (см. числитель). Деление на σ_Х и σ_y делает r безразмерным.