Методы корреляции порядковых (ординальных) и номинальных (категориальных) переменных
Бывает важно установить, есть ли между качественными признаками статистическая связь. Например, связан ли характер стружкозавивания при точении Xi с оцениваемым визуально качеством обработанной поверхности Yi или с условиями труда станочника Zi. Или связаны ли характер стружкозавивания с удобством её транспортировки.
Характеристика силы связи между качественными признаками носит название ранговой корреляции.
Такой анализ имеет большое значение. Например, если установлена высокая ранговая корреляция между двумя качественными признаками изделий, то можно контролировать изделия только по одному из признаков, что удешевляет и ускоряет контроль.
Для проведения оценки этой связи необходимо в первую очередь ранжировать рассматриваемые признаки каждого объекта, то есть присвоить им ранг. Например, рассматривается связь характера стружкозавивания при точении Xi с качеством обработанной поверхности Yi. Для каждого i - ого из, например, десяти различных опробованных режимов обработки оценивается степень стружкозавивания Xi по диаметру витка стружки или по экспертной оценке (см. ниже), если при некоторых режимах стружка вообще не завивается, а к примеру, ломается. Соответственно для каждого i - ого из этих десяти режимов обработки оценивается качеством поверхности Yi. Для этого можно использовать визуальную экспертную оценку, или присвоить ранги качества в соответствии с результатами контроля шероховатости: чем меньше шероховатость (Ra или Rz), тем выше ранг качества поверхности. Шкалы рангов степени стружкозавивания Xi и качества поверхности Yi должны быть одинаковыми, то есть изменяться в целочисленных значениях, например, от 1 до 10. Получим две последовательности рангов:
по признаку X: х1, х2, ..., хn;
по признаку Y: у1 , у2, …, уn.
Например, такие:
хi 1 2 3 4 5 6 7 8 9 10
yi 6 4 8 1 2 5 10 3 7 9
Здесь номера i первого признака (степени стружкозавивания) располагаются в порядке увеличения рангов, но это необязательно; важно лишь, чтобы хi соответствовало yi,то есть чтобы значения рангов по разным признакам отвечали одному i- ому режиму обработки.
Коэффициент ранговой корреляции Спирменаrs рассчитывается: 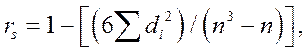 ( ),
( ),
где di = xi - yi.
Коэффициент rs заключен между -1 и +1, причем чем ближе к нулю его абсолютная величина, тем зависимость между качественными признаками X и Y меньше.
Для рассматриваемых значений X и Y по формуле ( ) коэффициент ранговой корреляции Спирмена rs = 0,32. Возможна строгая проверка значимости коэффициента ранговой корреляции Спирмена
Выдвигаем нулевую гипотезу Hо: коэффициент ранговой корреляции rs Спирмена равен нулю; при конкурирующей гипотезе rs не равен нулю.
Вычисляем критическое значение:
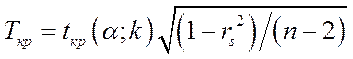 (13.15)
(13.15)
где n - объем выборки; rs - выборочный коэффициент ранговой корреляции Спирмена; tкр (α; k) - критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента по уровню значимости α и числу степеней свободы k = п - 2.
Если |rs| < Tкр, то нет оснований отвергнуть нулевую гипотезу, т.е. ранговая корреляционная связь между качественными признаками незначима.
Если |rs| > Tкр, то нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.
Для нашего случая находим: k= 10 - 2 = 8, tKp(α; k) = 2,31. Следовательно, Tкр = 0,773, и так как |rs| < Tкр, то нет оснований отвергнуть нулевую гипотезу, согласно которой ранговая корреляционная связь между признаками незначимая.
Кроме представленного выше коэффициента и критерия значимости ранговой корреляции Спирмена используют и другие коэффициенты и критерии значимости ранговой корреляции. Перечислим наиболее известные:
- коэффициент r ранговой корреляции Кендалла также изменяется от -1 до +1; используется достаточно часто, т.к. в отличие от rs не требует пересчёта заново при необходимости учёта вновь поступающих величин по всем выборочным значениям;
- критерий Гёфдинга;
- критерий Ширахатэ является аналогом критерия значимости ранговой корреляции Спирмена, но более эффективен для малых выборок,
- критерий Фишера-Йэйтса;
- критерий Ван дер Вардена.
Мощности коэффициентов ранговой корреляции несколько уступают мощности параметрического коэффициента корреляции.
- коэффициент корреляции знаков Фехнера Kф принципиально отличается от рассмотренных выше коэффициентов корреляции. Обычно его используют в оценке степени влияния одного параметра на другой по количеству совпадений и несовпадений знаков отклонений этих параметров от их среднего значения. То есть это оценка степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от средних значений факторного и результативного признаков.
Следует заметить, что коэффициент корреляции знаков Фехнера можно использовать для установления наличия или отсутствия действия какого-либо фактора, на результативный признак, причём обе характеристики выражены в номинальных случайных величинах. Например, требуется узнать, связано ли использование (+) или неиспользование (-) смазки при механической обработке на получение годной (+) или бракованной (-) детали.
Расчет коэффициента Фехнера производится по формуле:
Kф = (U - V)/(U + V)
где U - число пар, у которых знаки отклонений значений от их средних значений совпадают.
V - число пар, у которых знаки отклонений значений от их средних значений не совпадают.
Коэффициент Фехнера изменяется в пределах [-1;+1]. Из здравого смысла и формулы видно, что чем больше количество совпадений отклонений индивидуальных значений (U) и меньше количество несовпадений (V), тем в большей степени фактор оказывает положительное влияние на результативный признак (Kф приближается к 1). Наоборот, чем меньше количество совпадений отклонений индивидуальных значений (U) и больше количество несовпадений (V), тем в большей степени фактор оказывает отрицательное влияние на результативный признак (Kф приближается к минус единице). Оценка тесноты связи качественных признаков производится по таблице .
Таблица Оценка тесноты связи по коэффициенту Фехнера
| Значение коэффициента Фехнера | Качественная характеристика силы связи |
| [-0,9;-1] | Очень высокая обратная |
| [-0,7;-0,9] | Высокая обратная |
| [-0,5;-0,7] | Заметная обратная |
| [-0,3;-0,5] | Умеренная обратная |
| [-0,1;-0,3] | Слабая обратная |
| Связь отсутствует | |
| 0,1 - 0,3 | Слабая прямая |
| 0,3 - 0,5 | Умеренная прямая |
| 0,5 - 0,7 | Заметная прямая |
| 0,7 - 0,9 | Высокая прямая |
| 0,9 - 1 | Очень высокая прямая |
Дата добавления: 2016-01-26; просмотров: 2595;
