Области определения и способы оценки достоверности коэффициентов связи случайных величин
Коэффициент ковариации (2.1) имеет размерность, равную произведению размерностей случайных величин, и может изменяться от от +∞ до -∞. Безразмерный коэффициент корреляции r (2.2) - (2.4), колеблющийся в пределах от -1 до +1, является более наглядной и чаще используемой характеристикой «тесноты» связи: чем выше |r|, тем «теснее» статистическая связь. При коэффициенте корреляции, равном ±1, статистическая связь «переходит» в точную функциональную зависимость между переменными.
Коэффициент детерминации, как следует из определения,изменяется от 0 до +1.
Степень «тесноты» связи случайных величин оценивают по так называемой шкале Чеддока (табл. 2.2).
Таблица 2.2. Шкала Чеддока
| Теснота связи | Коэффициент корреляции |rху| |
| Слабая | 0,1 - 0,3 |
| Умеренная | 0,3 - 0,5 |
| Заметная | 0,5 - 0,7 |
| Высокая | 0,7 - 0,9 |
| Весьма высокая | 0,9 - 0,99 |
Шкала Чеддока применима лишь для быстрой ориентировочной оценки «тесноты» связи. Чем выше |rху| по шкале Чеддока, чем «теснее» связь, тем более достоверно её существование. Но всё же шкала не даёт однозначного ответа о наличии связи, т.е. о значимости коэффициента корреляции, особенно если он занимает некое промежуточное положение, например в пределах |rху| = 0,3 - 0,7. Это объясняется тем, что кроме величины |rху| значимость коэффициента корреляции определяется ещё двумя важными факторами:
- числом точек n (или числом «степеней свободы») - чем больше число точек, тем точнее (и достовернее) определяется rху;
- принятым в отрасли «доверительной вероятности» (чаще всего берётся g = 95 %, что соответствует «уровню значимости» α= 0,05).
Между тем правильное определение достоверности связи случайных величин имеет для статистического анализа кардинальное значение. Поэтому разработано множество способов и критериев проверки значимости коэффициента корреляции. Приведём три таких критерия, потому что они дополняют друг - друга по n, α и используемым вспомогательным средствам.
1. При помощи критерия Стьюдента. Наблюдаемое значение критерия определяется по формуле
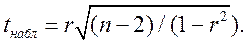 (2.5)
(2.5)
Критическое («табличное») значение (tкр) определяется по справочнику из таблицы t-распределения для принятого значения доверительной вероятности α и числа степеней свободы f = n - 2. (Для той же цели можно использовать статистическую функцию СТЬЮДРАСПОБР MS EXCEL.)
Если |tнабл| < tкр, то нет оснований отвергнуть нулевую гипотезу о том, что r = 0, т.е. о том, что связь величин не обнаружена. В противном случае (|tнабл| > tкр)нулевая гипотеза отвергается, т.е. можно считать, что для принятой доверительной вероятности связь величин установлена.
2. По ошибке коэффициента корреляции. (Способ ориентирован на обычно принимаемую доверительную вероятность α = 0,05.) Ошибку Sr оценивают по формуле
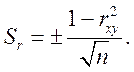 (2.6)
(2.6)
Далее определяется критерий существенности tr:
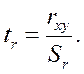 (2.7)
(2.7)
Если величина tr > 3, то коэффициент корреляции считается верным, т.е. связь между двумя случайными величинами является доказанной. И наоборот, если tr < 3, то полагают, что достоверная связь не установлена.
3. Табличный метод. Наиболее простой в использовании. Рекомендуем его, как наиболее простой не требующий каких-либо вычислений, в случаях, когда рассматриваемые n и α соответствуют приведённым в таблице. Если r > rкр (табл. ), делается вывод о существенности связи случайных величин с определённой доверительной вероятностью.
Таблица 217 Критические значения выборочного коэффициента корреляции rкр
| n | Доверительная вероятность | n | Доверительная вероятность | ||||
| 0,90 | 0,95 | 0,99 | 0,90 | 0,95 | 0,99 | ||
| 0,988 | 0,997 | 1,000 | 0,476 | 0,553 | 0,684 | ||
| 0,900 | 0,950 | 0,990 | 0,457 | 0,532 | 0,661 | ||
| 0,805 | 0,878 | 0,959 | 0,441 | 0,514 | 0,641 | ||
| 0,729 | 0,811 | 0,917 | 0,426 | 0,497 | 0,623 | ||
| 0,669 | 0,754 | 0,874 | 0,412 | 0,482 | 0,606 | ||
| 0,621 | 0,707 | 0,834 | 0,400 | 0,468 | 0,590 | ||
| 0,582 | 0,666 | 0,798 | 0,389 | 0,456 | 0,575 | ||
| 0,549 | 0,632 | 0,765 | 0,378 | 0,444 | 0,561 | ||
| 11 12 | 0,521 0.497 | 0,602 0.576 | 0,735 0.708 | 21 22 | 0,369 0..Ч60 | 0,433 0.423 | 0,549 0.S37 |
Дата добавления: 2016-01-26; просмотров: 1272;
