Множественная ранговая корреляция

До сих пор рассматривалась корреляция двух случайных величин, оцениваемых в рангах. Но бывают случаи, когда рассматривается корреляция сразу несколько таких случайных величин; требуется установить, насколько тесно они связаны. Наиболее часто необходимость проведения такой работы возникает, когда несколько экспертов оценивают в баллах (рангах) какой либо параметр или влияние какого-либо фактора, нескольких факторов и требуется выяснить, насколько эти оценки согласованы между собой.

Коэффициент конкордации (согласованности) является мерой связи нескольких случайных величин, оцениваемых в рангах. Он обычно используется для проверки согласованности мнений опрошенных специалистов.

Таким образом, метод множественной ранговой корреляции необходим начинаю­щему исследователю, собственные априорные сведения которого об исследуемом процессе, как правило, малы. Рассмотренный ниже коэф­фициент конкордации Кендалла-Бэмингтона Смита применим для любого количества случайных величин и их ранговых оценок (часто называется просто коэф­фициентом конкордации Кендалла). Существует также коэф­фициент конкордации Шукени-Фроли для двух групп специалистов-экспертов (здесь не рассмотрен).

Для подсчета коэф­фициента конкордации Кендалла используют выражение:

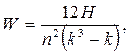
где n - число групп, которые ранжируются,

k - число переменных,

α_ij - ранг i- ого фактора у j- ого эксперта,

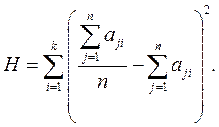Фактически это сумма квадратов отклонения суммы рангов рассматриваемых факторов от среднего значения суммы рангов всех факторов. (Здесь не рассматривается случай наличия так называемых "связанных рангов", при которых расчётные формулы становятся более громоздкими.)

Коэффициент конкордации позволяет определить, случайна или не случайна согласованность мнений специалистов: чем выше коэффициент конкордации, тем выше степень согласованности мнений специалистов. Коэффициент может принимать значения 0<W<1. Так, W=0 означает полное отсутствие согласованности между ранжировками специалистов, a W= 1 показывает, что специалисты одинаково расположили фак­торы.

Теория позволяет провести точную проверку значимости коэффициента конкордации, основанную на распределении хи-квадрат. Рассчитывается величина 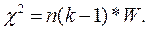Она сравнивается с критическим значением распределения для принятого уровня значимости α и числа степеней свободы f = (n-1)(k-1), определяемым из справочных таблиц. (Для этого можно использовать функцию MS EXCEL ХИ2ОБР.) В случае, если c²> c²_кр, то гипотеза об отсутствии связи отвергается, корреляция признаётся значимой. В противном случае гипотеза об отсутствии связи принимается.

Метод множественной ранговой корреляции позволяет, используя априорную информацию, отбросить несущественные технологические факторы, основываясь на опросе специалистов.

Этапы выявления влияющих факторов:

1. После анализа литера­турные источники об исследуемом процессе составляется пере­чень факторов, которые по сведениям этих источников могут ока­зывать влияние.

2. Возможно более широкому кругу специалистов (предста­вителям различных школ) предлагается расположить составленный перечень факторов в порядке убывания степени их влияния на выбранный выходной параметр исследуемого процесса. При этом представленный список факторов каждым из опрашиваемых специалистов может быть дополнен.

3. Результаты опроса представляют в виде таблицы - мат­рицы рангов, где для каждого фактора указывается место (значение а_ij), занимаемое им в анкете специалиста, номер которого или фамилия указывается в первом столбце матрицы.

Может быть принято такое правило: первое место (ему присваивается ранг а_ij = 1) соответствует наи­более существенному фактору. По мере уменьшения влияния фактора величина ранга а_ij возрастает. Чем меньше сумма рангов фактора, тем более высокое место он занимает в ранжировке, и, следовательно, большее влияние должен оказывать на выход­ной параметр.

Иногда матрица рангов строится с учетом квалифика­ции опрашиваемых специалистов, исходя из их опыта и всеобще­го признания, ставя на первое место специалистов, чье мнение вызывает наибольшее дове­рие (ранжиро­вание опрашиваемых). В этом случае показания специалистов умно­жаются на коэффициент, присваиваемый в соответствии с его квалификацией, а значение а_ijсоответствует результату этого пере­множения. Часто то или иное место в ранге специалистов может отда­ваться нескольким экспертам. Тогда им присваивается один и тот же коэффициент.

По полученной матрице рангов (рассчитанные значения суммы рангов занесены в третью снизу строку матрицы) строят диаграмму рангов. Если распределение на диаграмме рангов (рис 6.1а) равномерно, а изменение суммы рангов незначительно, то это зна­чит, что хотя специалисты и отводят неодинаковые места техно­логическим факторам в матрице рангов, но делают они это неуве­ренно. В этом случае целесообразно все факторы включить в эксперимент. При быстром экспоненциальном уменьшении степени влияния факторов (рис. 6.1,6) часть их можно отбросить.

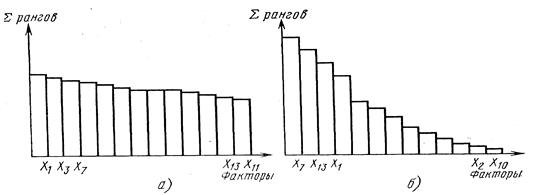
Рис. 6.1. Диаграммы рангов: а - равномерное распределение; б - экспоненциальное

3.2.5 Функции и инструменты MS EXCEL, предназначенные для расчёта коэффициентов ковариации, корреляции и детерминации

Наиболее важные и часто употребляемые аналитические характеристики достаточно просто определяются в рамках программы MS EXCEL. Так сходные по своим аргументам функции КОВАР и КОРРЕЛ (последняя представлена на рис. 2.3) определяют соответственно коэффициенты ковариации и корреляции по формулам (2.1) и (2.3). Для этого достаточно вставить массивы переменных и нажать ОК. Ту же задачу, что и функция КОРРЕЛ (имея те же аргументы), решает функция ПИРСОН. 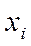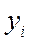Коэффициент парной линейной корреляции Пирсона в данном случае определяется по формуле (2.3), соответствующей для случая выборочных совокупностей и формуле (2.4). Таким образом, для выборок результаты расчётов по формулам КОРРЕЛ и ПИРСОН совпадают.

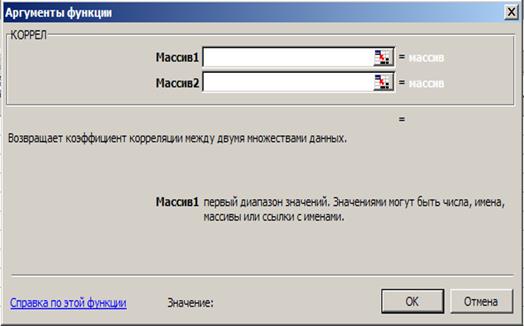
Рис. 2.3. Аргументы функции КОРРЕЛ

В MS EXCEL имеются также инструменты анализа «Ковариация» и «Корреляция», сходные своими диалоговыми окнами (последнее представлено на рис. 2.4). Они служат той же цели, что и соответствующие функции, но в отличие от функций в данном случае задаётся общий входной интервал с разделением анализируемых переменных по строкам или столбцам. При этом коэффициенты корреляции (или ковариации) рассчитываются для всех сочетаний задаваемых строк или столбцов. Таким образом, формируется так называемая «матрица корреляций» (или аналогично - «матрица ковариаций»).

В инструментах анализа имеется возможность выбора места выходного диапазона (рис. 2.4). При выводе результатов на текущий лист («Выходной интервал») введённая ссылка на ячейку указывает левую верхнюю ячейку выходного диапазона.

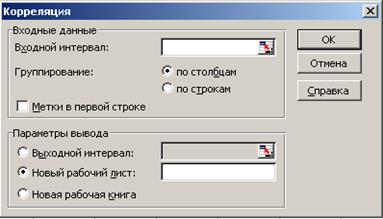
Рис. 2.4. Диалоговое окно инструмента анализа «Корреляция»

Статистическая функция КВПИРСОН (рис. 2.5) позволяет определять квадрат коэффициента Пирсона r² для парной линейной зависимости. Он представляет собой коэффициент детерминации для такого рода зависимости. Практическое использование коэффициента детерминации, показывающего степень аппроксимации экспериментальных точек аналитической зависимостью, особенно эффективно, когда эти аналитические зависимости можно оперативно изменять. Тогда появляется возможность выбрать такую зависимость, для которой установлен максимальный коэффициент детерминации. Эти возможности открываются при использовании графических опций MS EXCEL (глава 5).

Рис. 2.5. Аргументы функции КВПИРСОН