Однофакторный дисперсионный анализ
Дисперсионный анализ – это анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов.
Статистически проверить данное влияние можно с помощью критерия F Фишера. Он основан на вычислении вариативности исследуемого признака, обусловленной фактором (или факторами) и другими неизвестными переменными.
Данный критерий параметрический, так как в формулу расчета входят оценки дисперсий.
В дисперсионном анализе исследователь исходит из предположения, что одни переменные могут рассматриваться как причины (факторы), а другие – как следствия (результативный признак). Чаще всего исследователь сам формулирует для себя, что у него фактор, а что - результативный признак. При этом результативный признак обязательно должен быть представлен количественно, а фактор как качественно, так и количественно (но при этом количественные показатели факторы разбивают на группы, например, высокий, средний, низкий).
Каждый фактор должен иметь две или более градации, например: низкая, оптимальная и высокая мотивация достижения; низкий, средний и высокий уровень развития умения анализировать; принадлежность к полезависимому или поленезависимому когнитивному стилю; низкая и высокая скорость предъявления материала; мальчики и девочки; учащиеся младшего школьного, подросткого, юношеского возраста и т.д.
Вычисления:
с – количество условий (градаций фактора);
n – количество испытуемых в одной из групп;
N=c×n – общее количество индивидуальных значений;
Тсi – суммы индивидуальных значений по каждому из условий;
åTci2 - сумма квадратов суммарных значений по каждому из условий;
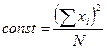 - отношение квадрата общей суммы индивидуальных значений к общему количеству индивидуальных значений.
- отношение квадрата общей суммы индивидуальных значений к общему количеству индивидуальных значений.
å(хi2) – сумма квадратов индивидуальных значений.
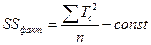 - вариативность признака, обусловленная действием исследуемого фактора.
- вариативность признака, обусловленная действием исследуемого фактора.
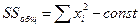 - общая вариативность признака.
- общая вариативность признака.
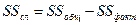 - вариативность, обусловленная неучтенными факторами (случайная вариативность).
- вариативность, обусловленная неучтенными факторами (случайная вариативность).
dfфакт=с-1 – число степеней свободы фактическое.
dfобщ=N -1 – число степеней свободы общее.
dfсл= dfобщ - dfфакт – число степеней свободы случайное.
 - фактическое математическое ожидание суммы квадратов.
- фактическое математическое ожидание суммы квадратов.
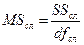 - случайное математическое ожидание суммы квадратов.
- случайное математическое ожидание суммы квадратов.
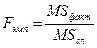 - эмпирическое значение критерия
- эмпирическое значение критерия
Сопоставим эмпирическое значение с критическими для df1=dfфакт и для df2=dfсл по таблице 13 приложения 2.
Если Fэмп³F0,01, то влияние фактора на признак значимо, если Fэмп <F0,05, то влияние фактора на признак не значимо, если F0,05 £ Fэмп < F0,01, то влияние фактора на признак достоверно лишь на 5% уровне значимости.
Пример. С детьми 6-7, 5-6 и 4-5 лет проводилось исследование произвольной образной памяти с помощью методики «запомни и найди такое же изображение предмета». Если ребенок показывал идентичное карточке изображение, то получал 3 балла, если изображение, схожее общим силуэтом и назначением – 2 балла, если совершенно другое изображение – 0 баллов. Максимально можно набрать 24 балла. Результаты представлены в таблице. Влияет ли возраст на уровень развития данного показателя?
Решение: фактором будет возраст (3 градации), а результативным признаком - балл по тесту на изучение произвольной образной памяти. Сформулируем экспериментальную гипотезу: возраст влияет на уровень сформированнности произвольной образной памяти.
Таблица 68
Результаты исследования произвольной образной памяти детей 4-7 лет и расчет некоторых данных по критерию F
| Дети 6-7 лет | Дети 5-6 лет | Дети 4-5 лет | |||
| № исп. | баллы | № исп. | баллы | № исп. | баллы |
| Тс1 | Тс2 | Тс3 | |||
| åxi=555 |
с=3; n= 10; N=c×n=30; Тс1=202; Тс2=181; Тс3=172; åTci2 =103149;
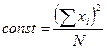 =10267,5; å(хi2)=10399;
=10267,5; å(хi2)=10399;
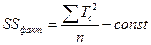 =47,4;
=47,4;
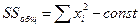 =131,5;
=131,5;
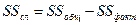 =84,1
=84,1
dfфакт=с-1=2; dfобщ=N –1=29;
dfсл= dfобщ - dfфакт= 27;
 =23,7;
=23,7; 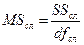 =3,11;
=3,11;
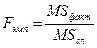 =7,62.
=7,62.
Для df1=dfфакт=2 и для df2=dfсл=27
F0,01=5,49; F0,05=3,35.
Fэмп >F0,01Þ принимается экспериментальная гипотеза.
Ответ: возраст влияет на уровень сформированнности произвольной образной памяти.
Дата добавления: 2016-01-26; просмотров: 976;
