Модель линейной регрессии
Изучение зависимостей экономических показателей начнем со случая двух переменных X и Y: Y=f(X). Этот метод наиболее прост и может быть представлен графически.
Для начала нужно установить, связаны ли эти переменные между собой, и, если да, то определить формулу связи. Для анализа данные представляют в виде таблицы:
| X | Y |
| x1 | y1 |
| x2 | y2 |
| ... | ... |
| xn | yn |
По таблице строим корреляционное поле (диаграмму рассеивания).
| yi |
| xi |
| y |
| x |
| Рис. 1 |
Точка с координатами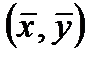 
называется центром рассеяния.
По виду корреляционного поля можно предположить, является ли зависимость между y и x линейной или нелинейной.
Значения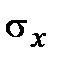 
(большие или малые) еще не дают характеристику того, если связь между х и у.
На рис.2 , рис.3 и рис.4 показана ситуация, когда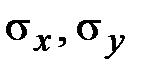 
малы, но в одном случае (рис.2) зависимости y=f(x) – нет. В другом случае зависимость есть и она линейная. В третьем случае есть явно нелинейная зависимость.
| x |
| y |
|
|
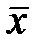
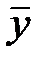
| Рис. 3 |
| x |
| y |
|
|
|
|
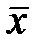
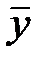
| Рис. 2 |
| x |
| y |
|
|
|
|
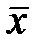
| Рис. 4 |
Поэтому вводится еще одна статистика коэффициент корреляции:
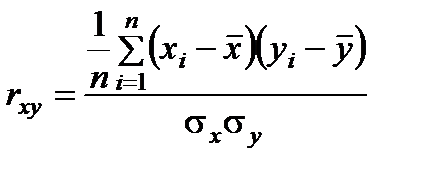
Коэффициент корреляции является показателем плотности линейной взаимосвязи.
Свойства коэффициента корреляции:
1) –1 £ rxy £ 1;
2) если rxy >0, то зависимость между фактором х и y прямая: с ростом х показатель y также возрастает. Если rxy <0, то зависимость между фактором х и y обратная - с ростом х показатель y уменьшается
3) Если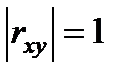 
связь между х и у – строго линейная. Если 
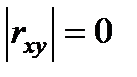, либо связи нет, либо связь резко нелинейная.
4) Коэффициент корреляции величина симметричная - rxy= ryx
5) Корреляция фактора самого с собой равна 1: rxx=1
Существует следующая градация тесноты линейной связи между Х и У в зависимости от величины коэффициента корреляции.
Если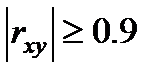 
то линейная связь между Х и У тесная.
Если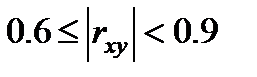 
то линейная связь между Х и У достаточная.
Если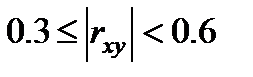 
то линейная связь между Х и У слабая.
Если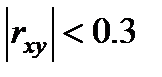 
то линейной связи между Х и У нет.
Подбор параметров прямой регрессии по методу наименьших квадратов (МНК)
Парной (однофакторной) линейной регрессией называется линейная зависимость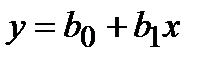 
между зависимым показателем Y и независимым фактором Х.
Пытаемся описать связь между х и у зависимостью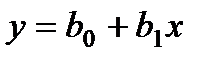 
(1).
В силу случайных влияний показатель yi является случайным и может быть выражен формулой
| yi=b0+b1xi+ei i=1..n | (2) |
ei – случайное отклонение.
Отклонение (ошибка) исходных данных yi от модельных данных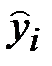 
=y(xi) вычисляется по формуле 
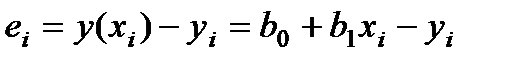. Обозначим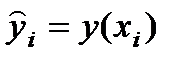 
| yi |
| xi |
| y |
| x |
|
|
| y=b0+b1x |
|
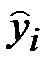
| ei |
Суть МНК состоит в том, чтобы минимизировать отклонения ei в совокупности путем правильного подбора коэффициентов b0 , b1.
Т.к. отклонение может иметь случайный знак (+ или -), то рассматривают квадраты отклонений. Минимизируют сумму квадратов отклонений
.
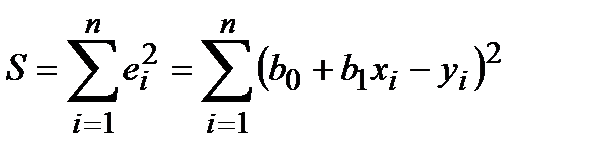Сумма S является функцией двух неизвестных параметров b0 , b1. Необходимое условие минимума функции S - равенство нулю производных по b0 и b1.
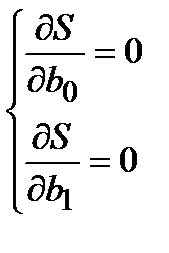
Получили систему двух линейных уравнений от двух неизвестных. Такая система имеет единственное решение.
Выразив коэффициенты b0 и b1, и, сделав арифметические преобразования, получим выражения для определения этих коэффициентов: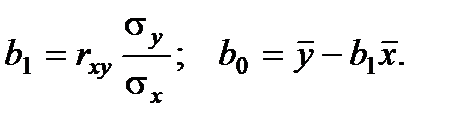 
Дата добавления: 2016-01-20; просмотров: 903;