Проверка с помощью критерия Фишера.

Выдвигаем гипотезу, что b₁=0. Т.е. уравнение регрессии будет иметь вид .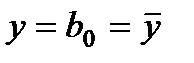

Для проверки этой гипотезы сравниваются между собой величины:

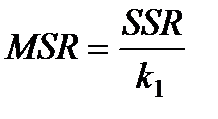и .

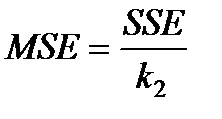Т.е. вычисляем дисперсию остатков 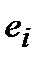и дисперсию расчетных данных 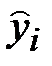, взятых с регрессионной прямой.

Вычисляем k₁, k₂ – количество степеней свободы для статистик MSR и MSE. Число степеней свободы k₁ равно числу независимых факторов в модели, k₂=n- k₁-1 (n- объем выборки).

Отношение введенных величин представляет собой наблюдаемое значение критерия Фишера со степенями свободы k₁, k₂. .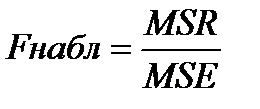

Переход от случая, когда мы можем признать F_набл.=0, а следовательно b₁=0 и зависимость у от х отсутствует, к случаю, когда следует признать F_набл.¹0 Þ b₁¹0 Þ есть зависимость у от х, производят, сравнивая F_набл с теоретически вычисленным критическим значением для критерия Фишера F_кр.

Рассчитывают точку F_кр, при некотором уровне значимости a и степенями свободы k₁, k₂. Уровень значимости – вероятность совершить ошибку.

Итак, сравним F_набл. с F_кр. и обнаружим, что F_набл< F_кр. - делаем заключение b1=0 Þ у от х не зависит Þ линейная регрессия неадекватна.

Если же F_набл. > F_кр, то гипотеза Н₀ отвергается, значит b₁¹0 Þ у зависит от х Þ линейная регрессия адекватна (с гарантией (1-a)×100%).

Иногда в ППП одновременно с вычислением наблюдаемого значения критерия, вычисляется его значимось a, т.е. вероятность совершить ошибку. Если это значение переобразовать в проценты, (a×100%), и полученное значение меньше 5%, то модель считается адекватной.