Алгоритм нахождения полуширины доверительного интервала.
На основании выборки
| x1 | x2 | … | xn |
| y1 | y2 | … | yn |
Получают уравнение регрессии 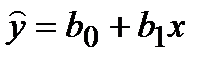 .
.
Доверительный интервал, в которое попадает неизвестное  с некоторым коэффициентом доверия g, как правило, в большинстве практических случаев оказывается симметричным относительно
с некоторым коэффициентом доверия g, как правило, в большинстве практических случаев оказывается симметричным относительно  .Поэтому, чтобы определить доверительный интервал, достаточно найти его полуширину d.
.Поэтому, чтобы определить доверительный интервал, достаточно найти его полуширину d.
При нахождении d используется специально сконструированная случайная величина, распределенная по закону Стьюдента с k=n-2 – числом степеней свободы .
Полуширина доверительного интервала в точке xпр вычисляется по формуле:
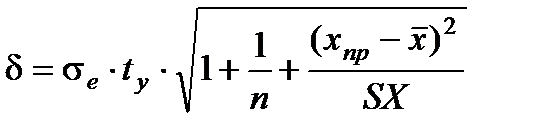
sе – средне квадратичное отклонение выборочных точек от линии регрессии 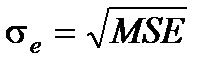
ty –критическая точка распределения Стьюдента, которая находится из таблиц для заданной надежности g (выбираем вероятность 1-g) и k2.
n – объем выборки
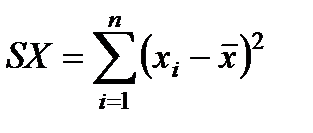 или
или 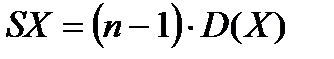
xпр – точка из области прогнозов.
Область прогнозов находится так: среди выборочных х находят xmin и xmax. Отрезок прямой, заключенный между ними называется областью прогнозов.
| xmin |
| xmax |
| Область прогноза |
Прогнозируемый доверительный интервал для любого х такой 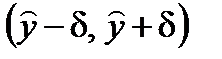
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область, которя представляет область заключения между двумя гиперболами. Наиболее узкое место в точке 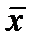 .
.
| y=b0+b1x |
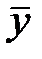
|
| xmin |
| xmax |
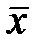
|
Прогноз для произвольного х дает интервал, в который с вероятностью g попадает неизвестное 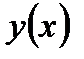 . Т.е. прогноз при заданном х составит от
. Т.е. прогноз при заданном х составит от  до
до 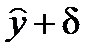 с гарантией
с гарантией 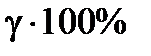 .
.
Дата добавления: 2016-01-20; просмотров: 5348;
