Нахождение регрессионной модели

Линейная многофакторная модель имеет вид: .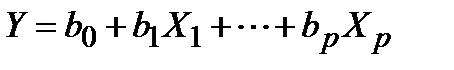

Параметры линейной многофакторной модели определяются по МНК. Только получаем систему p уравнений. Эту систему решают специальными методами матричной алгебры. Рассматривать эти методы не будем, т.к. неизвестные коэффициенты определим с помощью компьютера.

На этом этапе анализа появляются следующие сведения:

1. Коэффициент множественной корреляции: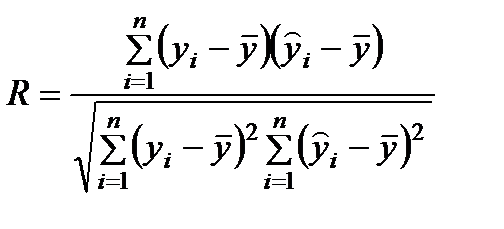

2. Коэффициент детерминации R².

3. Также считается уточненный коэффициент детерминации (adjusted R²) с учетом степеней свободы .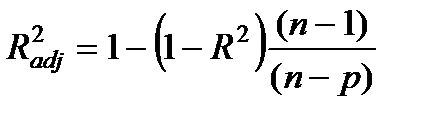

3. Наблюдаемое значение и степени свободы критерия Фишера. Для многофакторной регрессии гипотеза следующая: все коэффициенты b_i=0, кроме b₀.

Критерий Фишера в случае многофакторной регрессии имеет тот же смысл, что и в случае однофакторной регрессии, т.е. отношение двух дисперсий, однако число степеней свободы меняется: 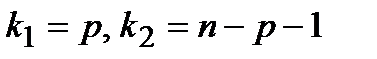. Здесь – p – количество факторов в модели, n – объем выборки.

4. Проверка значимости коэффициентов b_i.

Получили модель: .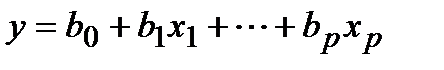

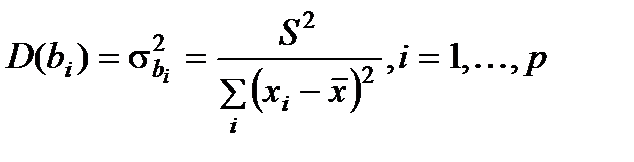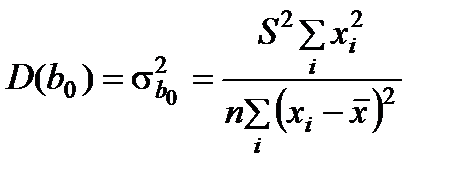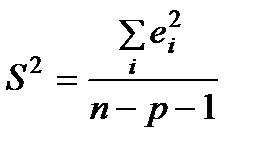Коэффициенты b_i - случайные величины. Их математические ожидания при выполнении некоторых условий равны соответственно точным значениям b_i. При этом, оценки тем надежнее, чем меньше их разброс вокруг точных значений, т.е. дисперсия. Можно доказать, что: , , где - дисперсия остатков.

Формально, значимость коэффициента b может быть проверена с помощью критерия Стьюдента: 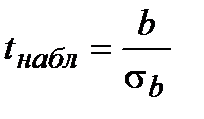. Если 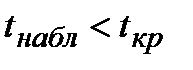, то коэффициент статистически не значим, т.е. данный фактор слабо влияет на показатель.