Матричная запись многофакторной регрессии
Данные для построения уравнения регрессии, сведем в таблицу:
Таблица 1
| № набл | Y | X1 | X2 | … | Xp |
| y1 | x11 | X12 | x1p | ||
| y2 | x21 | X22 | x2p | ||
| … | |||||
| n | yn | xn1 | Xn2 | xnp |
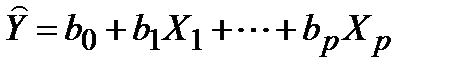 (1)
(1)
Подставляя в уравнение (1) значения из каждой строки таблицы, получим n уравнений.
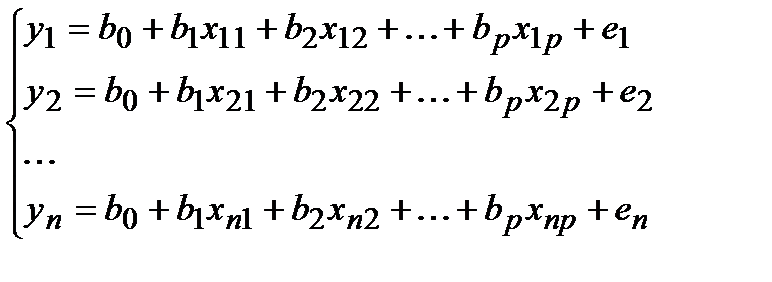 (2)
(2)
ei – случайные отклонения (остатки), наличие которых объясняется тем, что выборочные точки не ложатся в точности на плоскость (1), а случайным образом разбросаны вокруг нее. 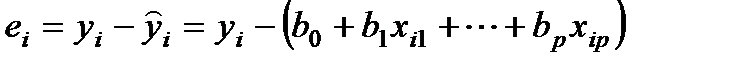
Чтобы записать систему (2) в матричном виде, вводим матрицу X, составленную из множителей при коэффициентах b1, b2, …, bp.
Матрица 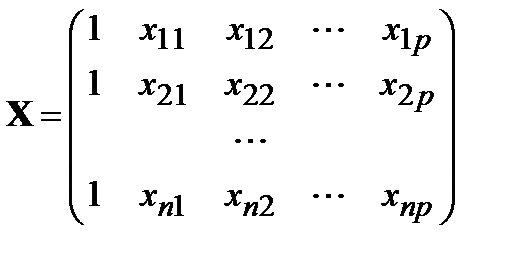 . Размерность матрицы n´p+1.
. Размерность матрицы n´p+1.
Еще вводятся матрицы:
Вектор столбец 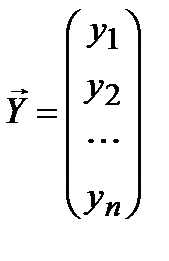 ,
, 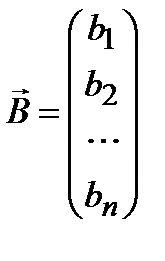 ,
, 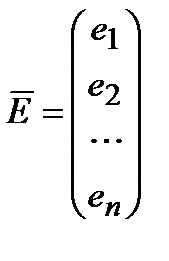 , размерностью n´1.
, размерностью n´1.
Тогда в матричной форме уравнение регрессии записывается так: 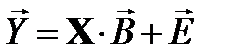 .
.
Полуширина доверительного интервала рассчитывается по формуле:
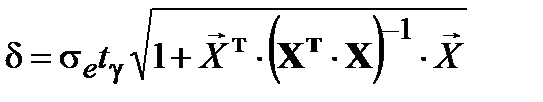 ,
,
где 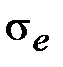 - среднее квадратическое отклонение остатков;
- среднее квадратическое отклонение остатков;
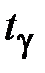 - критическая точка распределения Стьюдента, соответствующая уровню доверия g и степени свободы k=n-p-1.
- критическая точка распределения Стьюдента, соответствующая уровню доверия g и степени свободы k=n-p-1.
вектор 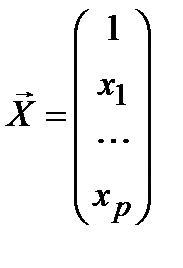 точка из области прогноза.
точка из области прогноза.
Нелинейная модель
Многие экономические процессы не могут быть адекватно описаны линейной зависимостью вида: y=b0+b1x.
Примером таких экономических процессов: жизненный цикл товаров, процесс накопления капитала, маркетинговые усилия фирм и др.
Наиболее часто используются 5 видов нелинейной зависимости, которые предпочтительней перед другими зависимостями тем, что их удается линеаризовать.
1. Степенная y=Axb
Обозначим V= Lny; u=Lnx; b0 =LnA и b1 =b.
Получили V= b0 + b1 u.
Обратное преобразование: V= LnyÞy=ev
A=eb0, b=b1.
2. Экспоненциальная =A×еbх
Обозначим V= Lny; u=x; b0 =LnA и b1 =b .
Получили V= b0 + b1 u.
Обратное преобразование: V= LnyÞy=ev
A=eb0, b=b1.
3. Логарифмическая зависимость y=A+Blnx.
Обычно используется, если значения фактора в несколько раз больше значений показателя.
Сделаем замену: V= y; u=Lnx; b0 =A и b1 =B. Получили V= b0 + b1 u.
Обратное преобразование: V= yÞy=v
A=b0, b=b1.
4. Гиперблическая зависимость 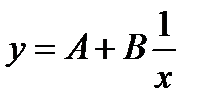
Сделаем замену: V= y; u= 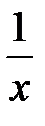 ; b0 =A и b1 =B. Получили V= b0 + b1 u.
; b0 =A и b1 =B. Получили V= b0 + b1 u.
Обратное преобразование: V= yÞy=v
A=b0, b=b1.
5. Степенная 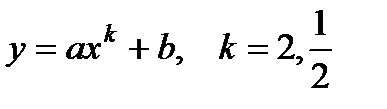
Сделаем замену: V= y; u= 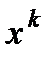 ; b0 =A и b1 =B. Получили V= b0 + b1 u.
; b0 =A и b1 =B. Получили V= b0 + b1 u.
Обратное преобразование: V= yÞy=v
A=b0, b=b1.
Дата добавления: 2016-01-20; просмотров: 999;
