При условии малости относительных перемещений найти

а) относительное удлинение волокон, в начальном положении параллельных оси 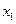, в малой окрестности частицы Мс координатами(1, 2, 2);

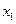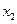б) величину изменения угла между волокнами, в начальном положении параллельными соответственно осям и , в малой окрестности точки М.

в) Увеличивается ли при деформации объем частицы среды в окрестности точки М?

1.17. Поле компонент вектора малых перемещений в декартовой системе координат таково:

.

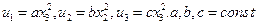При условии малости относительных перемещений

найти:

А) относительное изменение малых объемов при этих перемещениях;

б) изменение угла между волокнами, которые до деформации были параллельны, соответственно, осям 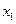и .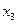

1.18. Поле компонент вектора малых перемещений таково:

При условии малости относительных перемещений вычислить:

А) компоненты тензора деформаций;

б) изменение угла между волокнами, которые до деформации были параллельны, соответственно, осям 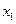и .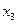

В) Проверить, что компоненты тензора деформаций удовлетворяют уравнениям совместности.