Покажем, что знание любого из введенных выше тензоров позволяет определить относительное удлинение произвольного волокна.

Действительно, согласно определению 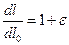, в то же время из определения Лагранжева тензора деформаций (1.4.3) и (1.4.4) можно получить следующее соотношение:

(1.4.7)

Отметим, что 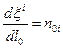- направляющие косинусы элементарного волокна 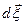в начальном состоянии, тогда из (1.4.7) следует:

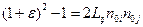или 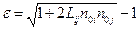(1.4.8)

Таким образом, для любого элементарного волокна 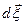деформация определяется выражением (1.4.8).

Аналогично можно оперировать Эйлеровым тензором деформаций тогда получим:

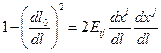(1.4.9)

Теперь обозначим направляющие косинусы элементарного волокна в текущем состоянии через 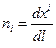тогда:

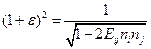или 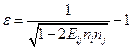(1.4.10)

Из общих соображений ясно, что деформации определяются перемещениями частиц и должна быть зависимость компонент тензоров деформаций от компонент вектора перемещений. Действительно из (1.2.1) и (1.4.4) следует:

(1.4.11)

Аналогично из (1.2.1) и (1.4.6) следует:

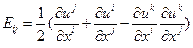(1.4.12)

В случае, если перемещения и, соответственно, деформации малы, а такое допущение используется довольно часто, лагранжевы и эйлеровы переменные отличаются мало, произведениями в формулах (1.4.11) и (1.4.12) можно пренебречь, для компонент тензора малых деформаций получаем:

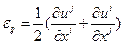(1.4.13)

Для геометрического истолкования смысла компонент тензора малых деформаций возьмем волокно 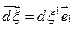, направленное вдоль первой оси, для него 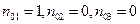и по формулам (1.4.8) и (1.4.13) получим:

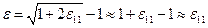(1.4.14)

Поскольку мы не ограничены в выборе системы координат и в нумерации осей, можно утверждать, что компоненты тензоров деформаций с одинаковыми индексами в случае бесконечно малых деформаций совпадают с коэффициентами относительных удлинений вдоль соответствующих декартовых осей координат начального состояния.

Обратимся к вопросу о геометрическом истолковании компонент 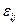с различными индексами (i≠j). Не нарушая общности, рассмотрим .

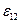Возьмем два волокна 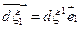и 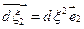, до деформации они взаимно ортогональны, найдем изменение угла 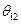между ними после деформации, когда они определяются векторами соответственно:

Из вышесказанного (1.4.14) следует, что текущие длины волокон равны соответственно:

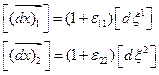
Посчитаем скалярное произведение этих векторов двумя способами и сравним результаты:

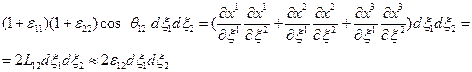(1.4.15)

Если ввести в рассмотрение угол 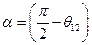равный изменению первоначально прямого угла между волокнам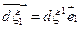и и 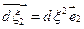то из соотношения (1.4.15) следует:

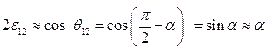(1.4.16)

Здесь вслед за перемещениями и деформациями мы предположили малость углов отклонения. Итак, мы получили, что в случае бесконечно малых деформаций компоненты 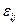(приi≠j) равны половине угла отклонения от первоначально прямого угла между соответствующими волокнами, направленными вi-том иj – том направлениях декартовой системы координат в процессе деформирования.

Следует отметить, что тензор деформаций – симметричный и как для всякого симметричного тензора второго ранга существуют главные оси тензора деформаций и в них отличными от нуля будут только диагональные элементы. Это означает, что всегда можно определить такую элементарную конфигурацию среды, которая деформируется только растяжением (сжатием) своих сторон, не изменяя углов. Такой конфигурацией является прямоугольный параллелепипед со сторонами направленными вдоль главных осей тензора деформаций. Рассмотрим относительное изменение объема при деформировании такого элементарного параллелепипеда. В начальный и текущий моменты времени этот объем равен соответственно:

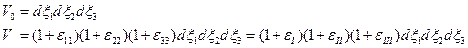(1.4.16)

Откуда получаем:

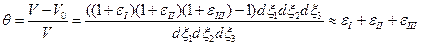(1.4.17)

Здесь 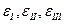- главные значения тензора деформаций, поскольку след матрицы, соответствующей тензору деформаций, является скалярным инвариантом тензора, мы можем заключить, что 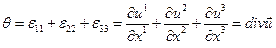является объемной деформацией.

§ 5. Тензор скоростей деформаций. Тензор вихря.

Геометрические характеристики деформаций важны в основном для твердых тел. В жидкостях и газах характеристики деформаций сами по себе играют гораздо меньшую роль. Например, перелитая из сосуда в сосуд жидкость (если она однородна) остается все такой же жидкостью, хотя при переливании в ней могли произойти сколь угодно сложные и сильные деформации. В жидкостях и газах свойства деформаций существенно проявляются только через изменения объемов. Соответственно, тензор деформаций играет основную и определяющую роль в теории деформирования твердых тел. В теории движения жидкости и газа - гидродинамике (и теории деформирования некоторых твердых тел) большую играет роль другая характеристика - тензор скоростей деформаций. Может быть так, что сами деформации несущественны, однако существенно, насколько быстро они происходят.

Применение векторного оператора пространственного градиента к векторному полю скорости дает тензор второго ранга 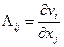(здесь и далее индексы будут писаться внизу, поскольку для векторов и тензоров в декартовых системах координат это не принципиально, а мы будем работать в основном с последними). Этот тензор можно раз­ложить на симметричную и антисимметричную части следующим образом:

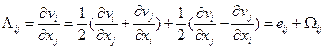или 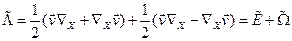(1.5.1)

Симметричный тензор 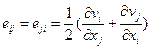или 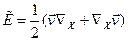(1.5.2)

называется тензором скоростей деформации. Антисимметричный

тензор 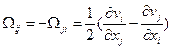или 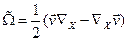(1.5.3)

называется тензором завихренности, или вихря.

Легко показать, что тензор скоростей деформации представляет собой материальную производную по времени от эйлерова тензора линейных (малых) деформаций (1.4.13). Так, если в выражении

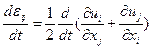(1.5.4)