Поменять местами операции дифференцирования по координатам, и по времени, то указанное равенство примет вид
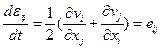или 
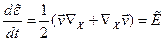(1.5.5)
Таким же образом можно показать, что тензор вихря равен материальной производной по времени от эйлерова тензора линейного поворота (антисимметричная часть пространственного градиента векторного поля перемещения).
Довольно интересную интерпретацию можно придать равенству (1.5.5), если переписать его в форме 
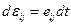или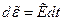 
(1.5.6)
Левая часть (1.5.6) представляет собой компоненты тензора, который широко используется в теории пластичности и называется тензором приращения деформации.
Важно подчеркнуть, что тензор деформаций вводится в результате сравнения двух состояний сплошной среды, а тензор скоростей деформаций является характеристикой данного состояния в данный момент времени.
|
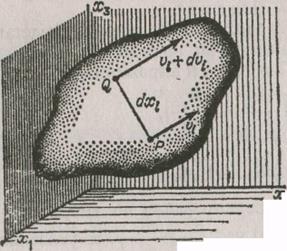
На рисунке проекции скорости соседних частиц, находящихся в точках P и Q движущегося объема сплошной среды, обозначены соответственно 
и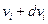 
. Таким образом, компоненты скорости частицы в точке Q относительно точки Р равна 
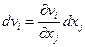, или 
, где частные производные вычислены в точке Р. Это выражение можно записать через компоненты тензоров скоростей деформаций и завихренности: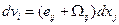 
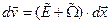(1.5.7).
Если тензор скоростей деформации тождественно равен нулю, то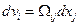 
или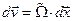 
(1.5.8)
и движение в окрестности точки Р будет вращением абсолютно твердого тела. Аналогично поле скоростей называют безвращательным или безвихревым, если тензор завихренности обращается в нуль во всех его точках.
Ассоциированный с тензором завихренности вектор определяется соотношением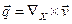 
или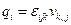 
(1.5.9)
и называется вектором завихренности. Символическая форма записи (1.5.9) показывает, что вектор завихренности получается действием оператора ротор rot на поле скоростей. Вектор 
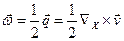равный половине вектора 
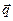называется вектором вихря скорости.
В малой окрестности любой частицыPсплошной среды для скоростей всех близких частиц имеет место следующая формула Коши-Гельмгольца
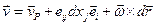(1.5.10)
здесь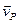 
- скорость частицыР(эту частицу можно условно назвать центром), 
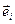- элементы базиса декартовой системы координат, 
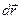- радиус-вектор близкой относительноРчастицы, 
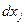- компоненты вектора 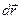и 
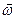- вектор вихря. Последний член в правой части этой формулы есть скорость за счет вращения частицы с мгновенной угловой скоростью 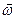. Формула Коши-Гельмгольца утверждает, что в малой окрестности любой частицы сплошной среды движение представляет собой сумму поступательного движения центра, движения, связанного с деформированием (второй член в правой части), и вращения с угловой скоростью. Если бы частица не деформировалась, то второй член в правой части формулы был бы равен нулю, и формула превратилась бы в известную формулу Эйлера для распределения скоростей в абсолютно твердом теле. В этом случае все материальные отрезки в частице вращались бы с мгновенной угловой скоростью 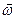. За счет деформации разные отрезки в частице поворачиваются с разными угловыми скоростями или не поворачиваются вовсе. Существенно также, что если среда при движении деформируется, то вектор 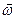в разных точках разный.
Если вектор вихря во всех точках равен нулю, то движение называется безвихревым. Можно доказать, что для безвихревого движения существует потенциал скорости, то есть такая функция 
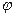, что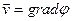 
. Такое движение называется потенциальным.
Физический смысл компонент тензора скоростей деформации можно увидеть из соотношения (1.5.5). Так диагональные элементы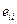 
— это скорости относительного удлинения отрезков, расположенных вдоль осей координат. Недиагональные элементы 
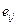характеризуют скорости сдвига и являются мерой скорости изменения прямых углов между направлениями отрезков, расположенных вдоль осей координат.
Вследствие того, что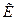 
является симметричным тензором второго ранга, для него существуют такие понятия, как главные оси, главные значения, инварианты, поверхность скоростей деформации и девиатор скоростей деформации. Кроме того, для компонент тензора скоростей деформации можно написать уравнения совместности, аналогичные уравнениям, полученным для тензора линейных деформаций.
§ 6. Материальные производные по времени от
Дата добавления: 2015-12-29; просмотров: 887;