картину движения, что угол между этими отрезками меняется, диагональный отрезок поворачивается.
1.24. Доказать, что 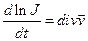 .
.
1.25. Поле скорости в некоторой среде имеет вид:
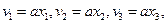 а > 0- константа.
а > 0- константа.
Увеличивается или уменьшается плотность в индивидуальных частицах среды? Обосновать ответ.
1.26. В трубе с неполным заполнением сечения течет несжимаемая однородная жидкость (нефть).Направим ось хвдоль оси трубы. Обозначим площадь живого сечения потока (т.е. сечения, занятого жидкостью) черезS(t,х),среднюю по живому сечению скорость вдоль оси трубы черезv(t,х).ВеличиныS, v меняются во времени и вдоль трубы из-за нестационарной работы насосов. Получить дифференциальное уравнение, связывающее S и v, рассматривая закон сохранения массы для пространственного объема между двумя близкими поперечными сечениями трубы.
Приложение. Понятие тензора как инвариантного объекта.
Инвариантность векторов. Для простоты ограничимся рассмотрением векторов в декартовых системах координат. В данной системе координат вектор 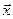 можно разложить по элементам базиса
можно разложить по элементам базиса 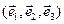 :
:
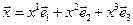 (п.1.1)
(п.1.1)
Векторы базиса - объекты не совсем тензорные, так как определяются выбором системы координат и не инвариантны относительно последнего. Однако это устоявшаяся терминология и мы будем следовать традиции, хотя правильнее говорить репер или элементы базиса. В дальнейшем для упрощения записи примем соглашение, что в любом индексном выражении по повторяющемуся индексу происходит суммирование (правило Эйнштейна). Такой индекс называется немым. Если индекс в индексном выражении встречается один раз, он называется свободным. Соглашение о суммировании по немому индексу позволяет сильно упрощать запись, делая ее более компактной и (п.1.1) примет вид  .
.
После сделанных замечаний приступим к изучению понятия инвариантности вектора. Пусть наряду с системой координат 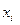 с базисом
с базисом 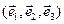 у нас есть еще одна система координат
у нас есть еще одна система координат  с базисом
с базисом 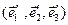 . Вектор
. Вектор 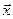 можно представить в каждой из введенных систем координат
можно представить в каждой из введенных систем координат 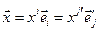 . Найдем закон преобразования компонент вектора. Для этого умножим последнее выражение скалярно на
. Найдем закон преобразования компонент вектора. Для этого умножим последнее выражение скалярно на 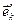 . В результате получим
. В результате получим 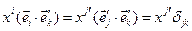 . Здесь
. Здесь 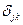 - символ Кронекера. Символ
- символ Кронекера. Символ 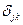 можно исключить из любого индексного выражения, но при этом необходимо положить во всем выражении j=k, тогда
можно исключить из любого индексного выражения, но при этом необходимо положить во всем выражении j=k, тогда  , а если ввести в рассмотрение матрицу
, а если ввести в рассмотрение матрицу 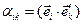 , то в матричном виде получим:
, то в матричном виде получим:
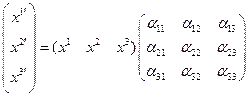 (п.1.2)
(п.1.2)
Аналогично найдем представление нового базиса 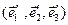 в старом базисе
в старом базисе 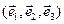 :
: 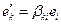 , где коэффициенты разложения
, где коэффициенты разложения 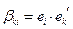 . Сравнение матриц
. Сравнение матриц 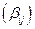 и
и 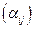 показывает, что
показывает, что 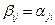 , т.е. матрица
, т.е. матрица 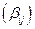 является транспонированной матрицей
является транспонированной матрицей 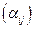 . Учитывая, что
. Учитывая, что  при фиксированном i представляют собой компоненты вектора
при фиксированном i представляют собой компоненты вектора 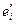 в базисе
в базисе 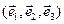 , получим:
, получим:
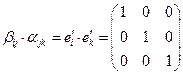
При переходе от одной декартовой системы координат к другой компоненты вектора преобразуются по закону (п.1.2), а элементы базиса при этом выражаются через элементы базиса старой системы координат по правилу 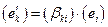 , причем матрицы перехода
, причем матрицы перехода 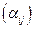 и
и 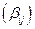 взаимно обратны
взаимно обратны 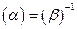 или
или 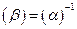 . Именно этим обеспечивается математически инвариантность вектора. Действительно, если определить вектор как математический объект, который задается в данной системе координат с базисом
. Именно этим обеспечивается математически инвариантность вектора. Действительно, если определить вектор как математический объект, который задается в данной системе координат с базисом 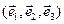 своими компонентами
своими компонентами  и потребовать, чтобы при переходе от старой системы координат к новой его компоненты определялись по закону (п.1.2), то данный объект не будет зависеть от системы координат, в которой он изучается. Действительно
и потребовать, чтобы при переходе от старой системы координат к новой его компоненты определялись по закону (п.1.2), то данный объект не будет зависеть от системы координат, в которой он изучается. Действительно
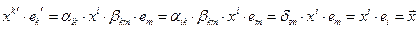 , то есть введенный объект инвариантен относительно преобразования координат.
, то есть введенный объект инвариантен относительно преобразования координат.
Тензоры. Обобщим полученные результаты на примере определения тензора второго ранга в декартовых системах координат. Возникает вопрос: нельзя ли, кроме 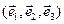 , ввести еще какие-нибудь базисные объекты, которые подобно
, ввести еще какие-нибудь базисные объекты, которые подобно 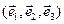 , управляя числами, позволили бы ввести еще более сложные, чем вектор, понятия, инвариантные относительно преобразования координат? Такие объекты можно ввести и в частности взять базисные объекты
, управляя числами, позволили бы ввести еще более сложные, чем вектор, понятия, инвариантные относительно преобразования координат? Такие объекты можно ввести и в частности взять базисные объекты 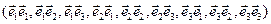 , которые называются полиадными произведениями элементов базиса (в данном случае диадными, поэтому их называют диадами или диадиками). Полиадное (тензорное или неопределенное) умножение векторов представляет собой некоторую операцию над векторами, приводящую к новым объектам (не векторам и не скалярам). Для определения этой операции достаточно указать ее свойства. В частности, существенен порядок перемножения векторов
, которые называются полиадными произведениями элементов базиса (в данном случае диадными, поэтому их называют диадами или диадиками). Полиадное (тензорное или неопределенное) умножение векторов представляет собой некоторую операцию над векторами, приводящую к новым объектам (не векторам и не скалярам). Для определения этой операции достаточно указать ее свойства. В частности, существенен порядок перемножения векторов 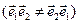 .
.
Определение. Тензором второго ранга назовем математический объект 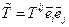 , который задан своими компонентами
, который задан своими компонентами 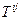 в разложении по базисным диадам, причем при переходе к другой системе координат его компоненты изменяются по закону
в разложении по базисным диадам, причем при переходе к другой системе координат его компоненты изменяются по закону 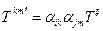 (п.1.3)
(п.1.3)
Покажем, что закон преобразования обеспечивает инвариантность объекта относительно выбора системы координат. В частности при переходе в декартовых системах координат, согласно (п.1.3) 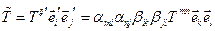 . Матрицы
. Матрицы 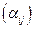 и
и 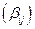 взаимно обратны и
взаимно обратны и 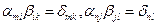 , тогда
, тогда 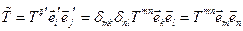 .
.
Таким образом, мы показали, что определенный нами объект не зависит от выбора системы координат, его запись инвариантна. Отметим, что в качестве базисных элементов можно было бы использовать триады  или в общем случае полиадные произведения n векторов базиса. В этом случае соответственно ранг тензора равен 3 для триад и n в общем случае. То есть рангом тензора называется число используемых векторов в базисных элементах.
или в общем случае полиадные произведения n векторов базиса. В этом случае соответственно ранг тензора равен 3 для триад и n в общем случае. То есть рангом тензора называется число используемых векторов в базисных элементах.
Определение. Тензором n-ного ранга называется объект 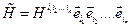 , компоненты которого
, компоненты которого 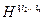 преобразуются при переходе к новой системе координат по закону
преобразуются при переходе к новой системе координат по закону 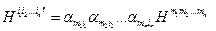 .
.
Число компонент тензора определяется его рангом и размерностью пространства, в котором он рассматривается. Для трехмерного пространства число компонент тензора равно 3ⁿ.
Операции над тензорами. Определим операции над тензорами любого ранга на примере тензора второго ранга. Естественно было бы ожидать, что они аналогичны операциям, определенным над векторами, но и не только, ведь уже при введении операций над векторами получилось число значительно больше, чем количество операций над скалярами. Сложение декартовых тензоров. Декартовы тензоры одинакового ранга можно складывать (или вычитать) покомпонентно. Сумма тензоров есть тензор того же ранга, что и слагаемые.

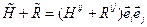
Умножение тензора на скаляр. Результат операции тензор того же ранга.
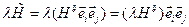
Скалярное умножение тензора на вектор (правое и левое). Результатом операции является тензор, ранг которого на 1 меньше, чем у первоначального. При скалярном умножении тензора 2--го ранга на вектор в результате получим вектор 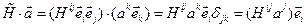
Отметим, что в общем случае 
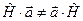
Векторное произведение тензора на вектор (правое и левое). Результатом операции будет тензор того же ранга 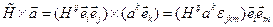 .
.
Отметим, что и в этом случае 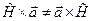 . Здесь были использованы символы Леви-Чивита
. Здесь были использованы символы Леви-Чивита 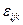 , определяемые соотношением
, определяемые соотношением 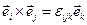 и равные 0, если хотя бы два индекса совпадают; 1, если тройка индексов ijk является четной перестановкой тройки 123; -1, если перестановка нечетна.
и равные 0, если хотя бы два индекса совпадают; 1, если тройка индексов ijk является четной перестановкой тройки 123; -1, если перестановка нечетна.
Неопределенное внешнее произведение тензоров. Результатом операции является тензор, ранг которого равен сумме рангов перемножаемых тензоров 
Внутренние операции, то есть операции без привлечения внешних объектов. Так над тензором второго ранга можно произвести операцию свертка (внутреннего скалярного произведения в его базисных диадах). Результатом операции является тензор на 2 меньшего ранга  .
.
Внутреннее векторное произведение, в результате получается  тензор на 1 меньшего ранга
тензор на 1 меньшего ранга 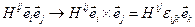 .
.
Cимметричные и антисимметричные тензоры второго ранга. Определенный интерес представляет симметрия тензора относительно перестановки его индексов.
Показать, что любой тензор второго ранга можно представить в виде суммы симметричного и антисимметричного тензоров.
Главные оси симметричного тензора второго ранга. Пусть 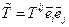 - симметричный тензор, и
- симметричный тензор, и 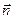 - главная ось (направление), тогда
- главная ось (направление), тогда
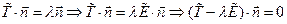 , где
, где 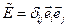 - единичный тензор.
- единичный тензор.
Нетривиальное решение существует, если 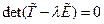 , что приводит к характеристическому уравнению тензора
, что приводит к характеристическому уравнению тензора 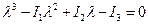 , где
, где  - инварианты тензора.
- инварианты тензора.
Дата добавления: 2015-12-29; просмотров: 770;
