Интеграла по подвижному объему.
Не все свойства среды можно задать для индивидуальной частицы функцией ее координат, некоторые свойства определяются интегралами по конечной части континуума. Пусть, например, какое-либо скалярное, векторное или тензорное свойство представлено интегралом по объему
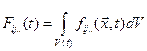, где 
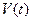— объем, который рассматриваемая часть сплошной среды (состоящая из одних и тех же частиц) занимает в момент времени t. Материальная производная от 
равна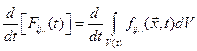 
, а так как интегрирование идет по определенной части континуума (т. е. индивидуализированной системе масс), операции дифференцирования и интегрирования можно менять местами. Итак, 
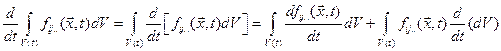(1.6.1)
Задача свелась к определению материальной производной от элемента индивидуального объема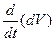 
.
|
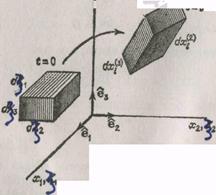
В результате движения из некоторого начального состояния в момент времени t=0 к рассматриваемому в момент времени t состоянию частицы сплошной среды, которые вначале занимали элементарный объем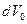 
, займут элементарный объем 
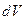. Если начальный элемент объема взят в виде прямоугольного параллелепипеда (рисунок), то, согласно (1.4.16),
. При движении этот параллелепипед перемещается и искажается, но из-за непрерывности движения не разрушается. Действительно, вследствие связи (1.4.1)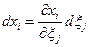 
между материальными и пространственными линейными элементами, волокно, которое раньше было 
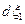, теперь образует бесконечно малый линейный отрезок 
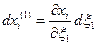. Аналогично 
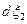переходит в 
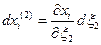, а 
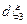- в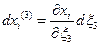 
. Поэтому бесконечно малый элемент объема 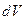представляет собой скошенный параллелепипед с ребрами 
, 
, 
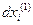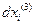. Величина его объема вычисляется как смешанное произведение
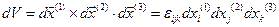. Очевидно, этот объем равен
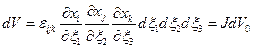(1.6.2)
где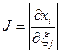 
— якобиан, определенный формулой (1.1.2).
Теперь, используя (1.6.2) и то, что 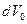от времени не зависит, можно получить материальную производную от 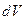по времени: 
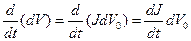(1.6.3)
Можно показать (см. задачу 1.24), что материальная производная от якобиана J равна
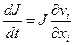или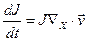 
(1.6.4)
и, следовательно, (1.6.3) принимает вид:
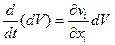или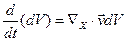 
(1.6.5)
После подстановки (1.6.5) в (1.6.1) приходим к следующему равенству:
(1.6.6)
А с учетом определения материальной производной (1.3.5) из последнего соотношения получим:
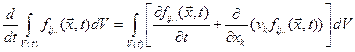(1.6.7)
По теореме Гаусса—Остроградского преобразуем второй член в правой части (1.6.7) в интеграл по поверхности, получим:
(1.6.8)
Это соотношение утверждает, что скорость изменения некоторой величины в части сплошной среды, занимающей в данный момент объем V , равна сумме изменении этой величины во всех точках внутри V плюс поток величины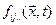 
через поверхность S, ограничивающую объем V .
Процедура определения материальных производных от интеграла по поверхности и линейного интеграла в общем та же, что только что проделанная для интеграла по объему.
§ 7. Закон сохранения массы. Уравнение неразрывности.
Всякий материальный континуум обладает свойством, называемым массой. Суммарная масса некоторой части сплошной среды, занимающей в момент времени t объем пространства V, выражается интегралом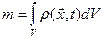 
(1.7.1) где 
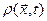— непрерывная функция координат, называемая плотностью.
Закон сохранения массы утверждает, что масса выделенной части среды остается постоянной и, следовательно, материальная производная от (1.7.1) равна нулю. Если в формуле (1.6.6) положить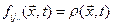 
, то получим выражение для скорости изменения массы m
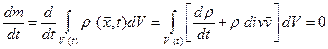(1.7.2)
Уравнение (1.7.2) является уравнением сохранения массы сплошной среды в интегральной форме, оно получено без всяких ограничений на функции, входящие в подинтегральные выражения. Ограничение одно - функции должны быть интегрируемыми. В частности, эти функции могут быть разрывными.
Потребуем теперь, чтобы все интересующие нас функции были непрерывно дифференцируемыми, тогда от уравнений в интегральной форме удается перейти к уравнениям в дифференциальной форме, более удобной для исследований. Тогда поскольку это равенство верно для произвольного объемаV,подинтегральное выражение само должно обращаться в нуль, т. е.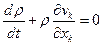 
или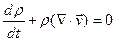 
(1.7.3)
Это уравнение называется уравнением неразрывности (или непрерывности). Раскрывая оператор материальной производной, его можно написать в другой равнозначной форме
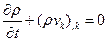или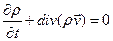 
(1.7.4)
В несжимаемой среде нет изменения расстояния между частицами и, следовательно, плотность массы каждой частицы не зависит от времени, т. е.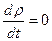 
или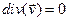 
(1.7.5)
Уравнение неразрывности можно записывать в лагранжевой, или материальной, форме. Для сохранения массы требуется, чтобы выполнялось уравнение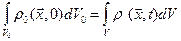 
(1.7.6)
Здесь оба интеграла взяты по одним и тем же частицам, т. е. V — это объем, который теперь занимает среда, заполнявшая в момент t = 0 объем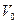 
. Используя (1.1.2) и (1.6.2), интеграл в правой части (1.7.6) можно преобразовать следующим образом:
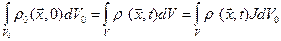(1.7.7)
Соотношение (1.7.7) должно иметь силу для произвольно выбранного объема 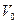, и поэтому 
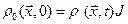,что означает, что произведение 
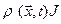не зависит от времени, так как объем V произволен, т. е. что
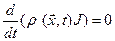(1.7.8)
Уравнение (1.7.8) является лагранжевой дифференциальной формой уравнения неразрывности.
ЗАДАЧИ к разделу кинематика.
Дата добавления: 2015-12-29; просмотров: 1906;