Понятие определенного интеграла
Определенный интеграл
Мы с вами узнали, что такое неопределенный интеграл - это совокупность первообразных заданной функции, т. е. множество функций. Интеграл является многогранным понятием, существует большое количество различного вида интегралов. Совершенно другим является понятие определенного интеграла, с которым мы сейчас познакомимся. Сразу отметим главное. Многие интегралы в своем определении являются пределами соответствующих сумм, называемых интегральными суммами. Результатом вычисления определенного интеграла, как и результатом вычисления многих других видов интегралов является число. Казалось бы, определенный интеграл кардинально отличается от интеграла неопределенного. Но на самом деле, вычисление того и другого сводится к нахождению первообразной заданной функции.
Понятие определенного интеграла
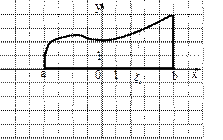
Пусть на отрезке 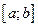 задана функция задана функция 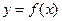 . Разделим этот отрезок точками . Разделим этот отрезок точками 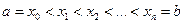 на на 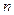 частей, длины которых равны соответственно числам частей, длины которых равны соответственно числам 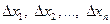 , где , где 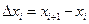 . На каждой из этих частей выберем произвольную точку . На каждой из этих частей выберем произвольную точку
| 
|
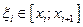 и рассмотрим сумму
и рассмотрим сумму 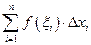 , (1) которая называется интегральной суммой.
, (1) которая называется интегральной суммой.
Определение 1. Определенным интегралом от функции 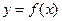 по промежутку
по промежутку 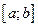 (обозначается
(обозначается 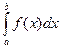 ) называется предел интегральных сумм (1), если этот предел существует и не зависит от способа разбиения области интегрирования
) называется предел интегральных сумм (1), если этот предел существует и не зависит от способа разбиения области интегрирования 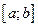 и выбора точек
и выбора точек 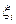 .
.
Для каких функций определенный интеграл существует, т. е. соответствующие функции интегрируемы на отрезке 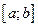 ? Для ответа на этот вопрос надо установить сходимость сумм Дарбу (1). Для этого надо рассмотреть верхнюю и нижнюю суммы Дарбу (значения функции
? Для ответа на этот вопрос надо установить сходимость сумм Дарбу (1). Для этого надо рассмотреть верхнюю и нижнюю суммы Дарбу (значения функции 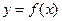 берутся соответственно самые большие и самые маленькие на каждом промежутке) и доказать, что разность между ними стремится к 0 при
берутся соответственно самые большие и самые маленькие на каждом промежутке) и доказать, что разность между ними стремится к 0 при 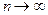 . Этот факт интегрируемости функции несложно установить для непрерывной функции на отрезке. Доказаны и более тонкие теоремы об интегрируемости монотонных и кусочно непрерывных функций.
. Этот факт интегрируемости функции несложно установить для непрерывной функции на отрезке. Доказаны и более тонкие теоремы об интегрируемости монотонных и кусочно непрерывных функций.
| <== предыдущая лекция | | | следующая лекция ==> |
| Взаимодействует с рецепторами клеток матрикса. | | | Понятие информационных технологий и их состав |
Дата добавления: 2015-12-16; просмотров: 551;
