Лекция 12.КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ, КАК ПРЕДЕЛ ИНТЕГРАЛЬНОЙ СУММЫ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Криволинейной трапецией называется геометрическая фигура, ограниченная графиком непрерывной неотрицательной функции y = f (x), отрезками прямых x = a и x = b и отрезком [a; b] оси OX.
Разобьем отрезок [a; b] на n‒ отрезков точками 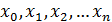 . На каждом отрезке
. На каждом отрезке 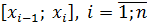 выбираем точку
выбираем точку 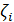 (кси),
(кси), 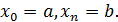
Построим прямоугольники с основанием: 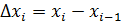 и высотой
и высотой
f( 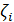 ), тогда
), тогда 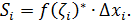 Сумма
Сумма 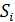 называется интегральной суммой.
называется интегральной суммой.

При 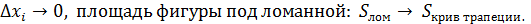 Получим:
Получим:
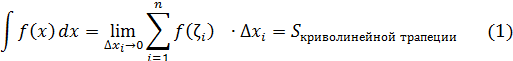
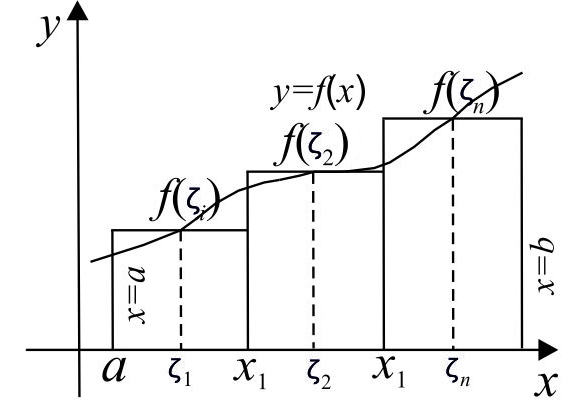
Рис. 1
Определенный интеграл, как предел интегральной суммы.
Геометрический смысл определенного интеграла.
Определенным интегралом от функции f (x) на промежутке [a; b] называется предел интегральной суммы(1).
Геометрический смысл.
Определенный интеграл от непрерывной неотрицательной функции
f (x) на промежутке [a; b] численно равен площади соответствующей криволинейной трапеции:
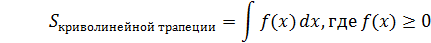
Геометрические приложения определенного интеграла.
1. Вычисление S фигуры.
1) Если геометрическая фигура ограничена графиками двух непрерывных неотрицательных функций 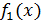 и
и 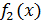 .
.
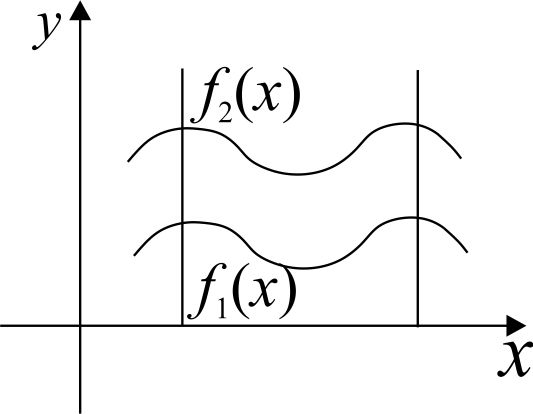
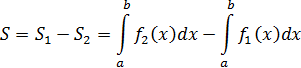
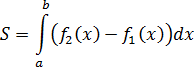
2) Если геометрическая фигура ограничена графиком 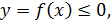
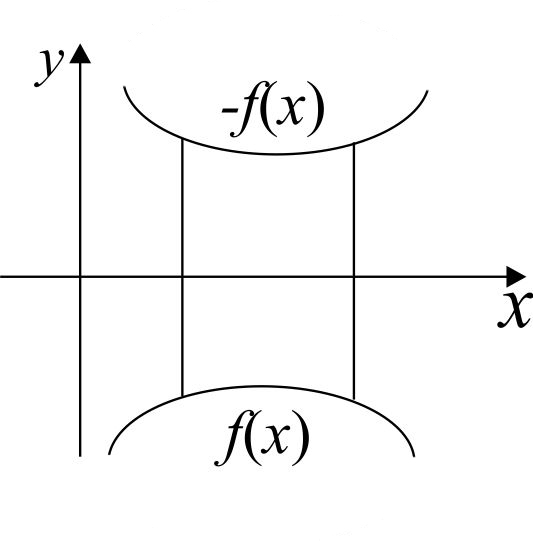
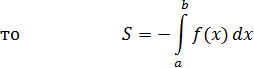
3) Если 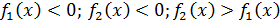
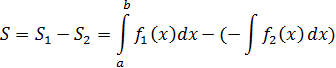
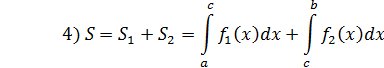
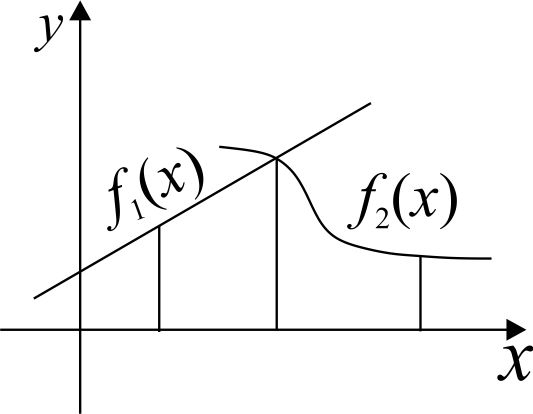
Пример.
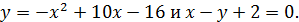
Решение:
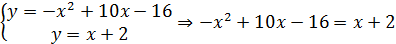
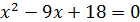
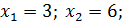
(3; 5), (6; 8) ‒ точки пересечения линии.
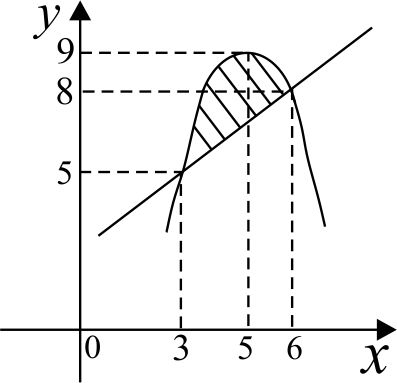
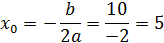
Второй способ:
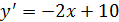
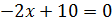
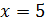
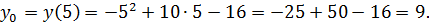
(5; 9) ‒ вершина параболы.
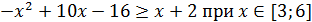
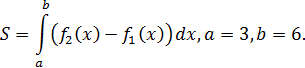
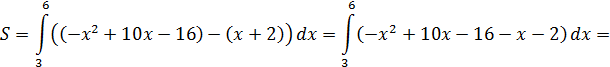
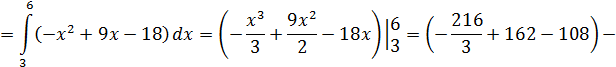
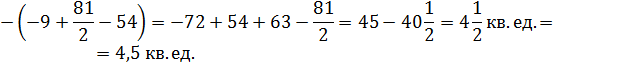
Дата добавления: 2015-12-16; просмотров: 1858;
