Материальная производная по времени.
Ясно, что математически точка зрения Эйлера отличается от точки зрения Лагранжа только тем, что в первой переменными являются координаты точек пространства 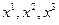 и время t, а во второй - параметры
и время t, а во второй - параметры 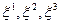 , индивидуализирующие точку сплошной среды, и время t.
, индивидуализирующие точку сплошной среды, и время t.
Переход от переменных Лагранжа к переменным Эйлера фактически реализуется соотношением (1.1.3), которое при фиксированных 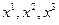 указывает те частицы (
указывает те частицы ( 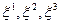 ) сплошной среды, которые в разные моменты времени приходят в данную точку пространства. Таким образом, если движение с точки зрения Лагранжа известно и его надо определить с точки зрения Эйлера, то для этого требуется только разрешить закон движения (1.1.2) относительно
) сплошной среды, которые в разные моменты времени приходят в данную точку пространства. Таким образом, если движение с точки зрения Лагранжа известно и его надо определить с точки зрения Эйлера, то для этого требуется только разрешить закон движения (1.1.2) относительно 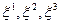 , т. е. записать его в виде (1.1.3); переход от движения, заданного по Лагранжу, к описанию движения по Эйлеру сводится только к разрешению неявных функций.
, т. е. записать его в виде (1.1.3); переход от движения, заданного по Лагранжу, к описанию движения по Эйлеру сводится только к разрешению неявных функций.
Наоборот, пусть с точки зрения Эйлера задано распределение скоростей в пространстве. Как найти закон движения, т. е. перейти к описанию движения по Лагранжу? Возьмем декартову систему координат 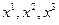 и пусть в ней известны компоненты скорости
и пусть в ней известны компоненты скорости 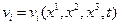 , которые в свою очередь являются производными от соответствующих координат по времени при постоянных параметрах
, которые в свою очередь являются производными от соответствующих координат по времени при постоянных параметрах 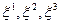 , индивидуализирующих точку сплошной среды. Поэтому на соотношения
, индивидуализирующих точку сплошной среды. Поэтому на соотношения
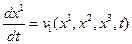
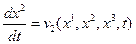 (1.3.1)
(1.3.1)

можно смотреть как на систему трех обыкновенных дифференциальных уравнений относительно 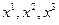 . Решив эту систему, найдем
. Решив эту систему, найдем 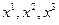 как функции t и трех произвольных постоянных
как функции t и трех произвольных постоянных 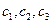 которые определяются по значениям
которые определяются по значениям 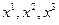 в некоторый данный момент
в некоторый данный момент 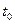 и, следовательно, являются параметрами, индивидуализирующими точку сплошной среды, - переменными Лагранжа. Таким образом, в результате решения этой системы дифференциальных уравнений находится закон движения (1.1.2), с помощью которого можно перейти от переменных Эйлера к переменным Лагранжа во всех формулах, определяющих распределения параметров. Следовательно, переход от переменных Эйлера к переменным Лагранжа при заданном поле скоростей связан, вообще говоря, с интегрированием обыкновенных дифференциальных уравнений.
и, следовательно, являются параметрами, индивидуализирующими точку сплошной среды, - переменными Лагранжа. Таким образом, в результате решения этой системы дифференциальных уравнений находится закон движения (1.1.2), с помощью которого можно перейти от переменных Эйлера к переменным Лагранжа во всех формулах, определяющих распределения параметров. Следовательно, переход от переменных Эйлера к переменным Лагранжа при заданном поле скоростей связан, вообще говоря, с интегрированием обыкновенных дифференциальных уравнений.
Ясно, что задания движения сплошной среды с точек зрения Лагранжа и Эйлера в механическом отношении эквивалентны друг другу и, например, любое физическое свойство континуума, приписанное индивидуальной частице (в лагранжевом, или материальном, описании), может также быть выражено для определенного места в пространстве, занятого этой частицей (в эйлеровом, или пространственном, описании). Скорость изменения со временем любого свойства в индивидуальных частицах движущейся среды называется материальной (или индивидуальной) производной по времени от этой величины. Материальную производную (также называемую субстанциональной или полной производной) можно представить себе как скорость изменения рассматриваемой величины со временем, которая была бы измерена наблюдателем, движущимся вместе с индивидуальной частицей. Мгновенное положение частицы 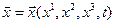 само является свойством этой частицы. Материальная производная по времени от положения частицы есть ее мгновенная скорость. Поэтому, принимая символ
само является свойством этой частицы. Материальная производная по времени от положения частицы есть ее мгновенная скорость. Поэтому, принимая символ 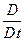 или точку над буквой для обозначения операции материального дифференцирования (в нашей литературе
или точку над буквой для обозначения операции материального дифференцирования (в нашей литературе 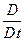 не широко применяется, чаще используется просто
не широко применяется, чаще используется просто  ), получаем определение вектора скорости этой частицы:
), получаем определение вектора скорости этой частицы:
 (1.3.2)
(1.3.2)
Вообще, если 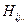 — любое скалярное, векторное или тензорное свойство среды - континуума, которое можно описать локальной функцией координат, и если в лагранжевом представлении
— любое скалярное, векторное или тензорное свойство среды - континуума, которое можно описать локальной функцией координат, и если в лагранжевом представлении 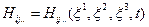 , то индивидуальная производная по времени от этой величины имеет вид
, то индивидуальная производная по времени от этой величины имеет вид 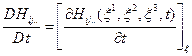 , то есть при лагранжевом материальном описании оператор
, то есть при лагранжевом материальном описании оператор 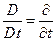 .
.
Если же некоторое свойство задано функцией 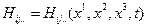 в пространственных переменных, то вычисление материальной производной приводит к выражению
в пространственных переменных, то вычисление материальной производной приводит к выражению
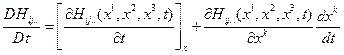 (1.3.3)
(1.3.3)
где второй член в правой части появляется из-за того, что индивидуальные частицы меняют свое местоположение в пространстве. Первый член в правой части (1.3.3) характеризует скорость изменения данного свойства в фиксированной точке пространства и соответственно называется локальной (или местной) скоростью изменения. Второй член в правой части равенства (1.3.3) называется конвективной скоростью изменения, так как он выражает вклад, обусловленный движением частиц в переменном поле данного свойства. Очевидно, что при эйлеровом, или пространственном, описании оператор 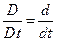 в классическом понимании полной производной, поэтому его еще называют полной производной в этом материальном смысле. Принимая во внимание (1.3.2), для индивидуальной производной можно написать
в классическом понимании полной производной, поэтому его еще называют полной производной в этом материальном смысле. Принимая во внимание (1.3.2), для индивидуальной производной можно написать
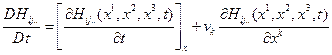 (1.3.4)
(1.3.4)
где 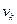 - k-ая компонента вектора скорости, что сразу наводит на мысль ввести оператор материального дифференцирования по времени
- k-ая компонента вектора скорости, что сразу наводит на мысль ввести оператор материального дифференцирования по времени
 (1.3.5) который используется при вычислении индивидуальных производных от величин, записанных в пространственных координатах.
(1.3.5) который используется при вычислении индивидуальных производных от величин, записанных в пространственных координатах.
Траекторией частицы ( 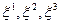 ) называется линия, по которой движется частица. При лагранжевом описании закон движения при фиксированных (
) называется линия, по которой движется частица. При лагранжевом описании закон движения при фиксированных ( 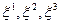 ) и переменном t представляет собой уравнение траектории частицы (в параметрическом виде). При эйлеровом описании траектории определяются дифференциальными уравнениями (1.3.1), которые можно записать так:
) и переменном t представляет собой уравнение траектории частицы (в параметрическом виде). При эйлеровом описании траектории определяются дифференциальными уравнениями (1.3.1), которые можно записать так: 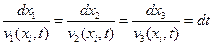 (1.3.6)
(1.3.6)
Линией тока называется определенная в данный момент времени линия, в каждой точке которой касательная направлена по вектору скорости 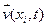 . Дифференциальные уравнения линии тока для момента времени
. Дифференциальные уравнения линии тока для момента времени 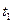 имеют вид
имеют вид 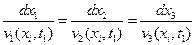 (1.3.7)
(1.3.7)
Установившимся, или стационарным, называется движение, при котором в каждой точке пространства, занятого средой, все ее характеристики не меняются со временем. При эйлеровом описании все параметры среды в этом случае не зависят явно от времени t . При установившемся движении линии тока не зависят от момента времени 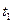 и совпадают с траекториями частиц.
и совпадают с траекториями частиц.
§ 4. Тензоры деформаций.
Рассмотрим два произвольных положения деформируемого тела и, в частности, его частиц M и M´ с координатами 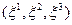 и
и  в начальный момент времени
в начальный момент времени 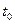 и координатами
и координатами
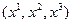 и
и 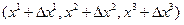 соответственно в момент времени t.
соответственно в момент времени t.
Векторы базиса декартовой системы отсчета наблюдателя обозначим через 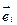 , а векторы базиса сопутствующей системы координат в момент времени t обозначим через
, а векторы базиса сопутствующей системы координат в момент времени t обозначим через  , тогда в начальный момент времени малый элемент сплошной среды M M´, называемый еще волокном , определяется вектором
, тогда в начальный момент времени малый элемент сплошной среды M M´, называемый еще волокном , определяется вектором 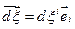 , а его начальная длина
, а его начальная длина 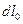 будет удовлетворять соотношению:
будет удовлетворять соотношению:
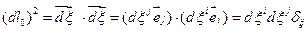
Важно отметить, что любой бесконечно малый материальный отрезок прямой (волокно), выходящий из частицы М, в процессе движения сплошной среды переходит в малый материальный отрезок прямой (любое волокно в процессе деформирования состоит из одних и тех же частиц). В текущий момент времени t то же волокно M M´ определяется вектором 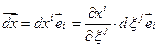 (1.4.1),
(1.4.1),
а его длина dl будет удовлетворять соотношению:
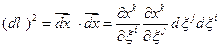
 (1.4.2)
(1.4.2)
Мы хотим ввести в рассмотрение характеристики изменения расстояний между частицами. Назовем коэффициентом относительного удлинения или относительной деформацией отношение 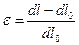
Коэффициент 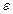 зависит от частицы М и направления элемента -волокна, для которого он вычисляется, и не зависит от длины
зависит от частицы М и направления элемента -волокна, для которого он вычисляется, и не зависит от длины 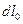 . Если
. Если 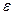 в каждой частице деформируемой среды и в каждом направлении бесконечно мал, то деформация называется бесконечно малой. Если
в каждой частице деформируемой среды и в каждом направлении бесконечно мал, то деформация называется бесконечно малой. Если 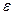 имеет конечное значение, то деформация конечная. По определению для абсолютно твердого тела все коэффициенты
имеет конечное значение, то деформация конечная. По определению для абсолютно твердого тела все коэффициенты 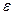 равны нулю.
равны нулю.
Вычислим разность квадратов длин:
 (1.4.3)
(1.4.3)
Назовем Лагранжевым тензором деформаций или тензором конечных деформаций Грина тензор с компонентами:
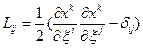 (1.4.4)
(1.4.4)
Аналогично можно посчитать длины волокна в системе наблюдателя, тогда:
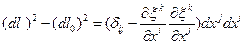 (1.4.5)
(1.4.5)
Соответственно Эйлеровым тензором деформаций или тензором конечных деформаций Альманси назовем тензор с компонентами:
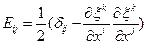 (1.4.6)
(1.4.6)
Тензоры деформаций являются тензорами второго ранга (векторы и скаляры не позволяют описать деформированное состояние сжимаемой среды) и служат основными характеристиками возникающих в телах деформаций, а их компоненты входят в основные уравнения, описывающие движение сплошной среды. Ясно, что в интересующий нас момент t величины деформации зависят не только от состояния тела, но и от того, по отношению к какому состоянию эти деформации вычисляются. Выбор этого начального состояния должен быть определен из конкретных физических соображений.
Дата добавления: 2015-12-29; просмотров: 3234;
