На изучение движения сплошной среды.
Как всякое движение, движение континуума всегда определяется по отношению к некоторой системе координат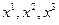 
- системе отсчета наблюдателя. Эта система координат может быть выбрана произвольно, и выбор ее зависит от исследователя. Частица движется относительно системы координат, если ее координаты меняются в зависимости от времени:
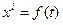(1.1.1)
Движущаяся частица в разные моменты времени отождествляется с разными точками пространства. Движение частицы известно, если известны функции (1.1.1), которые и называются законом движения частицы.
Сплошная среда представляет собой непрерывную совокупность частиц. По определению знать движение сплошной среды - это значит знать движение всех ее частиц. Ясно, что в деформируемой сплошной среде изучения движения объема как целого недостаточно. Для этого необходимы правила индивидуализации отдельных, совершенно одинаковых с геометрической точки зрения частиц континуума. Именами индивидуальных частиц сплошной среды можно, например, считать значения их начальных координат. Координаты точек в начальный момент времени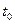 
будем обозначать 
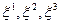, а координаты частиц в любой момент времени - 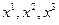. Тогда для любой частицы континуума, выделяемой координатами 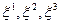можно написать закон движения, в который входят функции уже не одной, как в случае движения частицы, а четырех переменных - начальных координат 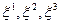и времени t:
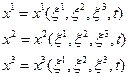(1.1.2)
Таким образом, основная задача кинематики заключается в определении функций (1.1.2), которые будем предполагать непрерывными и имеющими непрерывные частные производные по всем своим аргументам. Основываясь на соображениях физического характера, предположим, что в каждый фиксированный момент времени t=const функции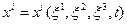 
являются взаимно однозначными функциями. Как известно, в этом случае якобиан 
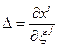не может обращаться в нуль во всех точках некоторого конечного объема, а если это так, то формулы (1.1.2) можно разрешить относительно 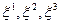и представить решение в виде однозначных непрерывных функций
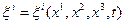(1.1.3)
Совокупность значений 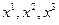образует в пространстве область D , занимаемую телом в данный момент времени t . Если координаты 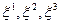рассматривать как значения координат 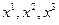в некоторый другой момент времени 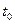, то область 
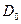изменений 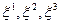соответствует объему, занятому телом в момент времени 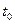. В этом случае закон движения (1.1.2) и (1.1.3) можно рассматривать как взаимно однозначное и непрерывное отображение областей D и 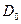. Как известно, общие топологические свойства таких преобразований заключаются в том, что любой объем переходит в объем , поверхность - в поверхность , линия - в линию , причем замкнутая поверхность переходит в замкнутую, а замкнутая линия - в замкнутую линию. Например, объем не может перейти в точку, так как при этом нарушилось бы условие взаимнооднозначности, а замкнутая линия не может перейти в незамкнутую линию, так как при этом нарушилось бы условие непрерывности.
Наряду с координатами 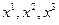координаты индивидуальных точек 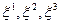можно рассматривать как другие координаты тех же точек пространства в области D. Соответствующая система координат 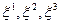в том же пространстве образует подвижную деформируемую криволинейную систему координат, которая называется сопутствующей системой координат. Так, если в начальный момент 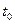выбрать в сплошной среде некоторые координатные линии 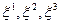, состоящие из частиц сплошной среды, то в следующий момент времени они вместе с точками континуума вновь перейдут в координатные линии сопутствующей системы. Однако если в начальный момент времени они и были выбраны прямыми, то в следующий момент они, вообще говоря, будут искривленными. Таким образом, если рассматривать систему координат, связанную с частицами сплошной среды, то она с течением времени будет изменяться. Выбор такой системы координат в любой данный момент времени в нашей власти, но в следующие моменты времени она уже не подвластна нам, так как она «вморожена» в среду и деформируется вместе с ней. Такая вмороженная в среду система координат и определена выше как сопутствующая система. Все частицы сплошной среды всегда покоятся относительно подвижной сопутствующей системы координат, так как их координаты 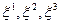в сопутствующей системе не меняются. Но сама система движется - растягивается, сжимается, извивается... Координаты 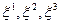индивидуализирующие частицы континуума и время t называются переменными Лагранжа, а использование в качестве независимых переменных 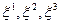и t составляет точку зрения Лагранжа на описание движения сплошной среды, которая, таким образом, существенно опирается на описание истории движения каждой частицы сплошной среды в отдельности. Такое описание на практике оказывается часто слишком подробным и сложным, однако оно всегда подразумевается при формулировке физических законов, так как они связаны с движением индивидуальных материальных частиц.
Дата добавления: 2015-12-29; просмотров: 771;