Скорость. Точка зрения Эйлера на изучение движения сплошной среды.

Кроме понятия закона движения, для описания движения сплошной среды необходимо ввести еще некоторые другие, в частности понятия перемещения, скорости и ускорения частиц. Для каждой частицы можно определить вектор перемещения, соединяющий начальное 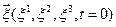и текущее 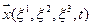положения данной частицы:

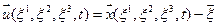(1.2.1)

Данное соотношение (1.2.1) как и (1.1.2) или (1.1.3) определяет закон движения сплошной среды. Рассмотрим близкие моменты времени t и t+Δt , за малое время Δt частица совершит малое перемещение 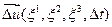. Определим вектор скорость частицы как предел отношения двух соответствующих бесконечно малых величин 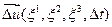и Δt при Δt →0 или частную производную вектора перемещения по времени ∂u/∂t и будем обозначать буквой .

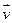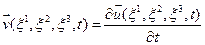(1.2.2)

Можно ввести понятие скорости без привлечения понятия перемещения через радиус-вектор 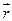частицы (в евклидовом пространстве это всегда возможно), который зависит в общем случае от трех параметров 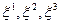, индивидуализирующих частицу сплошной среды, и времени t, тогда: 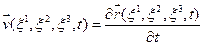(1.2.3)

Скорость вычисляется относительно системы отсчета. Очевидно, что относительно сопутствующей системы координат среда покоится, и поэтому скорость относительно сопутствующей системы всегда равна нулю.

Кроме скорости требуется, рассматривать еще вектор ускорения 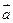частицы сплошной среды, который определяется так:

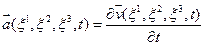(1.2.4)

Ускорение 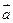, как и скорость 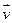, вычисляется для индивидуальной частицы сплошной среды.

Предположим теперь, что нас интересует не история движения индивидуальных частиц сплошной среды, а то, что происходит в разные моменты времени в данной геометрической точке пространства, связанного с системой отсчета наблюдателя. Пусть наше внимание концентрируется на данной точке пространства, в которую приходят разные частицы сплошной среды. Это и составляет сущность точки зрения Эйлера на изучение движения сплошной среды. Например, движение воды в реке можно изучать, либо следя за движением каждой частицы воды от верховьев реки до ее устья (это будет точка зрения Лагранжа), либо наблюдая изменение течения воды в определенных местах реки, не прослеживая движения отдельных частиц воды вдоль всей реки (это точка зрения Эйлера).

Точка зрения Эйлера весьма часто употребляется в приложениях. Геометрические координаты пространства 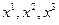и время t носят название переменных Эйлера. Движение, с точки зрения Эйлера, считается известным, если скорость и другие интересующие нас величины (например: ускорение, температура и т.п.) заданы как функции 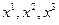и t:

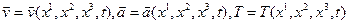(1.2.5)

Функции (1.2.5) при фиксированных 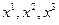и переменном t определяют изменения со временем скорости, ускорения, температуры и т. д. в данной точке пространства для разных приходящих в эту точку частиц. При фиксированном t и переменных 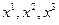эти функции дают распределения характеристик движения в пространстве в данный момент времени t; а при переменных 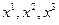и t - распределения характеристик движения в пространстве в разные моменты времени.

Таким образом, с точки зрения Лагранжа, мы интересуемся законами изменения скорости, ускорения, температуры и других величин для данной индивидуальной частицы сплошной среды, а с точки зрения Эйлера --- скоростью, ускорением, температурой и т. д. в данном месте. С точки зрения Эйлера, мы выделяем некоторую область пространства и хотим знать все данные о частицах, которые в нее приходят.

§ 3. Эквивалентность точек зрения.