Виды относительных величин

Наиболее распространенной является относительная величина, ко­эффициент или индекс динамики, который характеризует изменение какого-либо явления во времени, представляя собой отношение значений одной и той же абсолютной величины в разные периоды времени. То есть

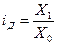. (1.1)

Здесь и далее подиндексы означают: 1 — отчетный или анализируемый период, 0 — прошлый или базисный период.

Критериальным значением индекса динамики служит единица. Если он больше ее, имеет место рост явления; равен единице — стабильность; если меньше единицы, наблюдается спад явления.

Еще одно название индекса динамики — индекс изменения, вычитая из которого единицу получают темп изменения с критериальным значени­ем нуль. Если он больше нуля, имеет место рост явления; равен нулю — стабильность; если меньше нуля, наблюдается спад явления.

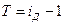. (1.2)

В некоторых учебниках по Статистике индекс изменения назван темпом роста, а темп изменения — темпом прироста, независимо от получаемого ре­зультата, который может показать стабильность или спад.

Если анализируемый и базисный периоды не являются соседними во временном ряду (например, год, предшествующий пятилетке и ее по­следний год), то найденный по формуле (1.1) индекс динамики или из­менения будет общим, поэтому дополнительно определяется средний индекс по формуле

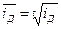, (1.3)

где t — количество периодов во временном ряду (например, в пятилет­ке t = 5).

Как и у общего, у среднего индекса критериальным значением слу­жит единица с теми же выводами о характере изменения. Вычитанием из среднего индекса единицы получают средний темп изменения с кри­териальным значением нуль и аналогичными выводами о характере из­менения явления.

На производстве применяются относительные величины, коэффици­енты или индексы планового задания и выполнения плана. Первый опре­деляется как отношение значений одной и той же абсолютной величины по плану анализируемого периода и по факту базисного. То есть

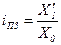, (1.4)

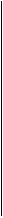где X’₁ — план анализируемого периода; X₀ — факт базисного пе­риода.

Индекс выполнения плана представляет собой отношение значений одной и той же абсолютной величины по факту и по плану анализируе­мого периода, определяясь по формуле

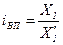(1.5)

Перемножая индексы планового задания и выполнения плана, полу­чаем индекс динамики. То есть

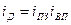(1.6)

Широко применяется также относительная величина, коэффициент или индекс структуры в виде отношения какой-либо части абсолютной величины ко всему ее значению. По существу это упоминавшаяся выше доля, удельный вес, частость, определяемая по формуле

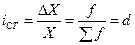. (1.7)

Например, если количество лиц женского пола (лжп) в группе сту­дентов поделить на численность всей группы, то получится индекс структуры лжп.

Похожей является относительная величина, коэффициент или индекс координации как отношение какой-либо части абсолютной величины к другой ее части, принятой за основу. Определяется по формуле

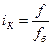. (1.8)

Например, если за основу принять количество лжп в группе студен­тов и на это число поделить количество лиц мужского пола (лмп) в ней, то получится индекс координации лмп относительно лжп.

Следующей является относительная величина, коэффициент или ин­декс сравнения в виде отношения значений одной и той же абсолютной величины в одном периоде или моменте времени, но для разных объек­тов или территорий. Определяется по формуле

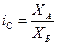, (1.9)

где А, Б — признаки сравниваемых объектов или территорий.

Еще один вид относительных величин сравнения получают путем сопоставления индексов динамики разных явлений. В результате образуются индексы опережения или отставания в развитии одного явления по сравнению с другим. Так, если на предприятии производительность труда увеличилась на 12 %, а средняя зарплата только на 7,5 %, то рост производительности труда опережает рост зарплаты по индексу изменения на 112/107,5=1,042 или на 4,2 %, а по темпу изменения на12/7,5=1,6 или на 60 %. Это и есть соответствующие индексы опережения. Индекс отставания роста зарплаты от роста производительности труда будет обратной величиной.

Перечисленные индексы являются безразмерными относительными величинами, а показателем, имеющим размерность, служит относительная величина интенсивности в виде отношения значений двух разнородных абсолютных величин для одного периода времени и одной территории или объекта. Для ее определения используется формула

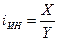. (1.10)

К показателям интенсивности относятся упомянутые выше себе стоимость, цена, энергоемкость продукции и другие относительные величины с дробной размерностью.