Правила применения средней арифметической и гармонической взвешенных

Они часто применяются для осреднения относительных величин ин­тенсивности, т.е. показателей, имеющих дробную размерность. При этом соблюдаются следующие правила.

1. Если имеются дополнительные данные по числителю дробной размерности, то применяется средняя гармоническая.

2. Если имеются дополнительные данные по знаменателю дробной размерности, то применяется средняя арифметическая.

3. Если неясно, к числителю или знаменателю относятся дополни­тельные данные, то поочередно применяются средняя гармоническая и арифметическая, а затем определяется средняя между ними величина.

Для иллюстрации правил решим задачу: 4 фирмы выпускают одинаковую продукцию при себестоимостях в руб/ед.: Si = 5, 3, 4, 6, а доли фирм равны соответственно di = 0,3; 0,2; 0,4; 0,1. Определить среднюю себестоимость продукции.

Для решения примера используем вышеизложенные правила.

1. Если доли фирм относятся к текущим затратам (числитель показателя себестоимости), то ее среднее значение определяем по формуле (1.16) как среднюю гармоническую величину

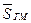= 1/ (0,3/5 + 0,2/3 + 0,4/4 + 0,1/6) = 4,1 (руб./ед.)

2. Если доли фирм относятся к количеству выпущенной продукции (знаменатель показателя себестоимости), то ее среднее значение находим по формуле (1.14) как среднюю арифметическую величину

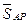= 5*0,3 + 3*0,2 + 4*0,4 + 6*0,1 = 4,3 (руб./ед.)

3. Если не сказано, к чему относятся доли фирм, то в дополнение к выполненным расчетам определяем среднюю себестоимость как простую среднюю величину из полученных результатов. То есть 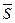= (Sгм + Sар)/2 = 4,2 (руб./ед.)

Таким путем рассчитываются средние значения и других показателей с дробной размерностью.