Виды степенных средних величин
Средние величины делятся на два больших класса: степенные и структурные. К последним относятся мода и медиана, но наиболее часто применяются степенные различных видов.
Степенные средние, в зависимости от представления отдельных величин, могут быть простыми и взвешенными. Простая средняя рассчитывается при наличии двух и более статистических величин, расположенных в произвольном порядке. Общая формула простой средней величины имеет вид
= 
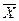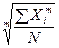.(1.11)
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы
= 
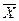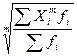(1.12)
При этом обозначено:
Xi – значения отдельных статистических величин или середин группировочных интервалов;
m - показатель степени, от значения которого зависят следующие виды степенных средних величин:
при m = -1 средняя гармоническая;
при m = 0 средняя геометрическая;
при m = 1 средняя арифметическая;
при m = 2 средняя квадратическая;
при m = 3 средняя кубическая и так далее.
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида. Так, приняв m = 1, находим, что простая средняя арифметическая величина определяется по формуле
= 
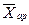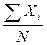. (1.13)
Аналогично для взвешенной средней арифметической величины получаем формулу через частоты или через доли (так как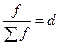 
)
= 
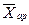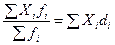. (1.14)
Не представляет трудностей и вывод формул для простых и взвешенных средних квадратических и кубических величин. Несколько сложнее вывод средней гармонической при m = –1. Так, используя формулу (1.11), имеем вначале
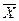гм = 
= 
,
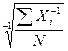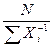а окончательно получим, что простая средняя гармоническая величина определяется по формуле
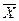ГМ =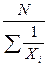 
, (1.15)
Аналогично выводится формула взвешенной средней гармонической величины, которая имеет следующий окончательный вид через частоты или через доли
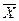ГМ =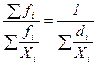 
, (1.16)
Наиболее часто употребляются формулы средних арифметических и гармонических величин.
Дата добавления: 2015-12-26; просмотров: 757;