Определение координат центра тяжести

В физике вводятся два понятия:

1) центр масс (центр инерции) – точка, характеризующая распределение масс в механической системе;

2) центр тяжести – точка, через которую проходит равнодействующая сил тяжести, действующих на все частицы этого тела.

Положение центра тяжести твёрдого тела совпадает с положением его центра масс.

Сила, с которой каждое тело притягивается к Земле, называется силой тяжести. Она распределена по всему объёму тела, т.е. приложена к каждой частице тела и направлена вертикально вниз к центру Земли (рис. 11.1). Элементарные силы тяжести этих частиц 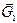, 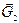… 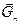практически параллельны и направлены вниз. То есть имеется система параллельных сил, выходящих из множества материальных точек:

, … .

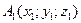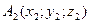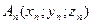Равнодействующая этих параллельных сил , называемая силой тяжести тела, приложена в точке С, являющейся центром тяжести тела. Таким образом, центром тяжести тела называется центр параллельных сил тяжести всех элементарных частиц тела.

Очевидно, что .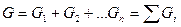

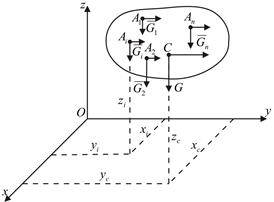
Рис. 11.1

Используя теорему Вариньона, найдём момент равнодействующей относительно оси Оу как сумму моментов составляющих сил относительно той же оси

.

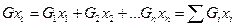Отсюда найдём координату центра тяжести x_c:

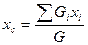. (11.1)

Аналогично из уравнения моментов относительно Ox найдём координату

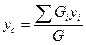. (11.2)

Затем мысленно повернём все силы против часовой стрелки на 90° и, используя уравнение моментов относительно оси Ох, получим

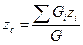. (11.3)

Однородная материальная линия. Тело, у которого два измерения (высота и ширина) пренебрежимо малы по сравнению с третьим измерением (длиной), называют материальной линией (например, стержень). У таких тел отношение силы тяжести G к длине l – постоянная величина для любого произвольного участка линии:

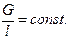
С учётом этого формулы (11.1) – (11.3) можно выразить так:

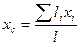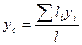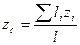, , . (11.4)

Однородная материальная поверхность. Материальной поверхностью называют тело, у которого одно измерение (толщина) пренебрежимо мало по сравнению с двумя другими (длиной и шириной). У однородной материальной поверхности отношение силы тяжести к площади поверхности есть постоянная величина для любой произвольной части поверхности

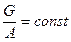. (11.5)

С учётом формулы (11.5) формулы (11.4) можно выразить так:

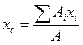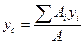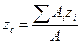, , , (11.6)

где А – полная площадь поверхности.

Однородный материальный объем. Материальный объем имеет соизмеримыми все три измерения. Для любой части однородного тела

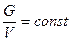. (11.7)

С учетом равенства (11.7) формулы (11.1 – 11.3) примут вид:

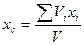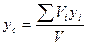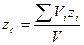, , , (11.8)

где V – полный объем тела.

Статический момент площади. Произведение площади фигуры S на расстояние от ее центра тяжести до какой-либо оси называют статическим моментом этой площади относительно данной оси. Так, 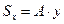– статический момент площади S относительно оси х,а 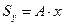– статический момент этой же площади относительно оси у. Чтобы определить статический момент площади сложной фигуры относительно некоторой оси, необходимо сложить статические моменты отдельных частей фигуры относительно этой же оси, т.е.

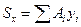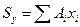, . (11.9)

Ось, проходящую через центр тяжести, называют центральной. Статический момент плоской фигуры относительно любой центральной оси равен нулю.