Методические указания к решению задач. При решении задач на равновесие, если имеются силы трения, рекомендуется придерживаться следующего порядка.
При решении задач на равновесие, если имеются силы трения, рекомендуется придерживаться следующего порядка.
1. Выделить тело или систему тел, равновесие которых необходимо рассмотреть.
2. Изобразить все активные силы.
3. Отбросить связи, заменив их реакциями. При этом реакцию шероховатости поверхности необходимо представить двумя составляющими: нормальной реакцией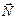 
и силой трения 
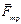. Иногда целесообразно полную реакцию не раскладывать на составляющие, а направить ее под углом трения j к нормали.
4. Сопоставить число неизвестных величин и число независимых уравнений равновесия, т. е. убедиться в статической определимости задачи.
5. Направить оси координат.
6. Составить систему уравнений равновесия для сил, действующих на тело.
7. Решить уравнения равновесия относительно искомых величин. Отметим, что основные указания по выбору координатных осей и моментных точек остаются такими же, как и для задач без трения.
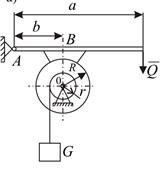
Пример 19. С помощью тормозного рычага равномерно опускают груз G = 2 кH. Определить усилие нажатия на рычаг Q, если радиус шайбы тормоза R = 0,2 м, радиус барабана r = 0,05 м, коэффициент трения f = 0,2, а = 4b (рис. 13.4, а).
|
|
| ||||||||||||||||||||||
|
|
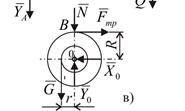
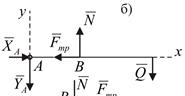
Рис. 13.4
Решение. Рассмотрим равновесие рычага (рис.13.4, б),находящегосяпод действием силы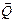 
,составляющих реакции в оси 
, 
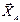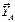, нормальной реакции шайбы тормоза 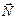и силы трения 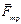. Составим уравнения моментов относительно А:
, 
,
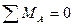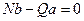откуда
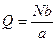. (a)
Теперь рассмотрим равновесие барабана (рис. 13.4, в). К нему приложены силы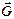 
, , , 
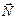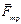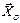и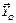 
. Составим уравнения моментов относительно оси барабана О:
, 
,
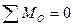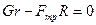откуда
,
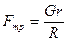и, следовательно,
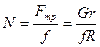. (б)
Подставляя выражение (б) в (а), получим
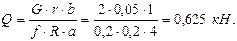
Дата добавления: 2015-12-26; просмотров: 614;