Методические указания к решению задач. При решении задач на равновесие произвольной пространственной системы сил рекомендуется придерживаться следующего порядка.
При решении задач на равновесие произвольной пространственной системы сил рекомендуется придерживаться следующего порядка.
1. Выделить тело, равновесие которого следует рассмотреть.
2. Изобразить активные силы.
3. Освободить тело от связей, заменив их реакциями. Число неизвестных не должно быть более шести, иначе задача статически неопределима.
4. Выбрать пространственную систему координат х, у, z.
5. Составить уравнения равновесия.
6. Решить полученные уравнения относительно неизвестных.
После решения необходимо произвести проверку, для чего рекомендуется составить сумму моментов всех сил относительно какой-либо оси, отличной от принятых для решения задачи осей х, у, z.
| |
|
|
| |
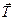 натяжения каната, если кран весом
натяжения каната, если кран весом 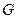 = 30 кН с грузом
= 30 кН с грузом 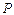 = 40 кH оттягивается горизонтальным тросом, переброшенным через блок и несущим противовес
= 40 кH оттягивается горизонтальным тросом, переброшенным через блок и несущим противовес 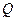 = 1,5 кH. Угол наклона каната к горизонту равен a = 60°. Трением в блоке пренебречь (рис.10.5, а).
= 1,5 кH. Угол наклона каната к горизонту равен a = 60°. Трением в блоке пренебречь (рис.10.5, а).

|
|
|


|
|
|
|


|
|
|
|
|


|

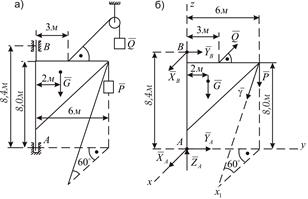
Рис. 10.5
Решение. Рассмотрим равновесие крана (рис. 10.5, б). К крану приложены следующие активные силы и реакции связей: силы тяжести крана 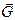 и груза
и груза 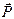 , реакция троса
, реакция троса 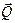 , реакция каната
, реакция каната 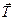 , реакции опоры В –
, реакции опоры В – 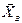 ,
, 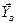 и реакции подпятника А –
и реакции подпятника А – 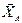 ,
, 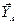 ,
, 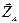 .
.
Направим, оси координат. Всего имеем шесть неизвестных: 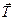 ,
, 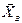 ,
, 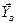 ,
, 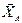 ,
, 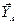 ,
, 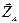 – задача статически определима. Составим шесть уравнений равновесия:
– задача статически определима. Составим шесть уравнений равновесия:
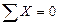 ,
, 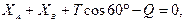 (а)
(а)
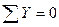 ,
, 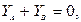 (б)
(б)
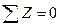 ,
, 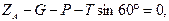 (в)
(в)
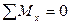 ,
, 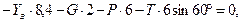 (г)
(г)
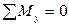 ,
, 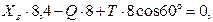 (д)
(д)
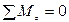 ,
, 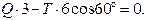 (е)
(е)
Из выражения (е) найдём реакцию каната, численно равную его натяжению:
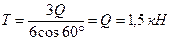
Решив уравнение (д), определим
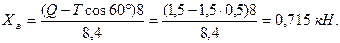
Из соотношения (в) найдём вертикальную составляющую реакции подпятника:
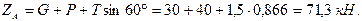
Решив уравнение (а), определим:
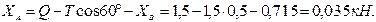
Из уравнения (г) следует, что
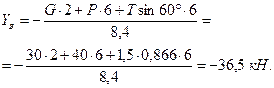
Из уравнения (б) имеем
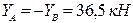 .
.
Направление 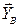 следует изменить на противоположное.
следует изменить на противоположное.
Для проверки составим сумму моментов относительно оси x1:
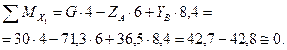
Дата добавления: 2015-12-26; просмотров: 977;
