МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ

Действие одной силы или системы сил на твёрдое тело может быть связано не только с поступательным, но и с вращательным движением. Как известно, силовым фактором вращательного движения является момент силы.

Рассмотрим гайку, которую затягивают гаечным ключом определённой длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то, прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное действие силы характеризуется моментом силы.

Понятие момента силы относительно точки ввёл в механику итальянский учёный и художник эпохи Возрождения Леонардо да Винчи.

Моментом силы относительно точки называется произведение модуля силы на ее плечо (рис. 5.1):

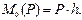(5.1)

Точка, относительно которой берется момент, называется центром момента. Плечом силы относительно точки называется кратчайшее расстояние от центра момента до линии действия силы.

Единица момента силы в системе СИ:

[М] = [Р] · [h] = сила ∙ длина = ньютон ∙ метр = Н∙м.

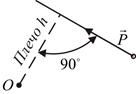
Рис. 5.1. Момент силы относительно точки

Условимся считать момент силы положительным, если сила стремится вращать свое плечо вокруг центра момента против часовой стрелки и наоборот (рис. 5.2).

Одна и та же сила относительно разных точек может давать и положительный и отрицательный момент (рис. 5.2).

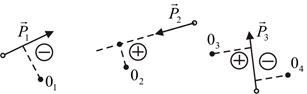
Рис. 5.2. Определение знака момента

Момент силы относительно точки, лежащей на линии действия этой силы, равен нулю, так как в этом случае плечо равно нулю.

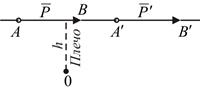
Рис. 5.3. Перенос силы вдоль линии действия

ПАРА СИЛ

Систему двух равных по модулю параллельных сил, направленных в противоположные стороны и не лежащих на одной прямой, называют парой сил (рис 6.1, а). Варианты обозначения пары сил приведены на рис. 6.1, б.

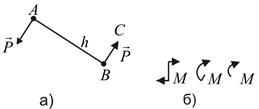
Рис. 6.1

Понятие пары сил введено в механику в начале XIX в. французским учёным Пуансо, который разработал теорию пар. Рассмотрим основные понятия.

Любые две силы, кроме сил, образующих пару, можно заменить равнодействующей. Пара сил не имеет равнодействующей, и никакими способами пару сил нельзя преобразовать к одной эквивалентной силе. Пара – такой же самостоятельный простейший механический элемент, как и сила.

Плоскость, в которой лежат силы, образующие пару, называют плоскостью действия пары. Кратчайшее расстояние между линиями сил, образующих пару, называют плечом пары h. Произведение модуля одной из сил пары на её плечо называют моментом пары и обозначают

М = ± Ph. (6.1)

Действие пары на тело характеризуется моментом, стремящимся вращать тело. При этом, если пара сил вращает тело против часовой стрелки, то момент такой пары считается положительным, если по часовой стрелке, то момент считается отрицательным.

Свойства пар

Не изменяя действия на тело, пару сил можно:

1) как угодно перемещать в её плоскости;

2) переносить в любую плоскость, параллельную плоскости действия этой пары;

3) изменять модуль сил и плечо пары, но так, чтобы ее момент (т. е. произведение модуля силы на плечо) и направление вращения оставались неизменными;

4) алгебраическая сумма проекций сил, образующих пару, на любую ось равна нулю;

5) алгебраическая сумма моментов сил, образующих пару, относительно любой точки постоянна и равна моменту пары.

Две пары считают эквивалентными, если они стремятся вращать тело в одну сторону и их моменты численно равны. Пару может уравновесить только другая пара с моментом, имеющим противоположный знак.

Сложение пар

Система пар, лежащих в одной плоскости или параллельных плоскостях, эквивалентна одной равнодействующей паре 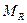, момент которой равен алгебраической сумме моментов слагаемых пар, т. е.

. (6.2)

Равновесие пар

Плоская система пар находится в равновесии, если алгебраическая сумма моментов всех пар равна нулю, т. е. .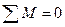

Часто бывает удобным представить момент пары в виде вектора. Вектор-момент пары направлен перпендикулярно к плоскости действия пары в сторону, откуда вращательное действие пары наблюдается против часовой стрелки (рис. 6.2).

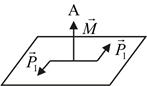
Рис. 6.2. Вектор-момент пары сил

Пример 7. На балку, свободно опирающуюся на гладкий уступ А и шарнирно укреплённую в точке В, действует пара с моментом М = 1500 Нм. Определить реакции в опорах, если l = 2 м (рис. 6.3, а).

Решение. Пару может уравновесить только другая пара с равным, но противоположно направленным моментом (рис. 6.3, б). Следовательно,

.

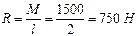Отметим, что независимо от того, где приложен внешний момент, реакции в опорах не изменяются (рис. 6.3, в, г).

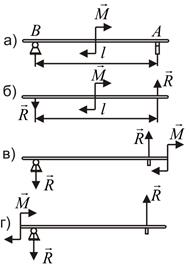
Рис.6.3

Контрольные вопросы

1. Чему равен модуль момента силы относительно точки?

2. Что представляет собой плечо?

3. Как определяют знак момента силы относительно данной точки?

4. Изменится ли знак и модуль момента, если силу переносить вдоль её линии действия?

5. Чему равен момент силы относительно точки, лежащей на линии действия этой силы?

6. Как определить направление вектора момента силы?

7. Какую систему называют парой сил?

8. Какое действие на тело оказывает пара сил?

9. Как определяют модуль и знак момента пары?

10. Можно ли пару либо систему пар уравновесить одной силой?

11. Перечислите свойства пар.

12. Чему равен момент равнодействующей пары?

13. Каково условие равновесия системы пар?