Плоская система произвольно расположенных сил
Приведение силы к данной точке. Действие силы на тело не изменяется, если ее перенести параллельно самой себе в произвольно выбранную точку О, приложив при этом пару сил, момент которой равен моменту данной силы относительно О. Такую пару называют присоединённой, а точку О – точкой приведения.
|
|
|

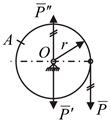
Рис. 7.4
Пусть к ободу колеса по касательной приложена окружная сила 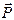 . Для определения действия этой силы на колесо и подшипники приложим к точке О уравновешенную систему сил
. Для определения действия этой силы на колесо и подшипники приложим к точке О уравновешенную систему сил 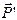 и
и 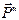 , причём
, причём 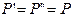 (по модулю). Тогда можно говорить, что мы заменили силу
(по модулю). Тогда можно говорить, что мы заменили силу 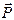 на
на 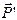 плюс пара сил
плюс пара сил 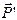 и
и 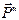 .
.
В результате получим силу 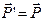 , вызывающую давление на подшипники, и пару сил (
, вызывающую давление на подшипники, и пару сил ( 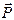 ,
, 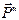 ) с моментом М = Р∙r, который будет вращать колесо.
) с моментом М = Р∙r, который будет вращать колесо.
Итак, при приведении силы 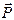 к точке
к точке 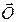 получается эквивалентная система, состоящая из силы, равной силе
получается эквивалентная система, состоящая из силы, равной силе 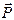 по модулю и направлению, и присоединённой пары.
по модулю и направлению, и присоединённой пары.
Приведение системы сил к данному центру. Пусть дана произвольная плоская система сил 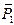 ,
, 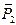 …
… 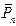 . Приводя все эти силы к произвольно выбранной точке О, называемой центром приведения, получаем n сил и n присоединённых пар.
. Приводя все эти силы к произвольно выбранной точке О, называемой центром приведения, получаем n сил и n присоединённых пар.
Геометрическую сумму сил произвольной плоской системы называют главным вектором 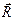 этой системы:
этой системы:
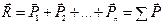 . (7.5)
. (7.5)
Главный вектор 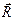 не изменяется с изменением центра приведения.
не изменяется с изменением центра приведения.
Алгебраическую сумму моментов сил произвольной плоской системы сил относительно какой-либо точки О называют главным моментом МО этой системы сил относительно точки О:
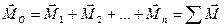 . (7.6)
. (7.6)
Главный момент изменяется с изменением центра приведения. Таким образом, плоская система сил в результате приведения к данному центру заменяется эквивалентной системой, состоящей из главного вектора и главного момента.
Теорема Вариньона. Момент равнодействующей плоской системы сил относительно любого центра, лежащего в плоскости действия этих сил, равен алгебраической сумме моментов сил данной системы относительно того же центра, т.е.
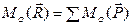 . (7.7)
. (7.7)
Эта теорема применима и для параллельных сил.
Применим теорему Вариньона для решения примера 8 (рис. 7.3). Приняв точку А за центр моментов, на основании теоремы Вариньона запишем:
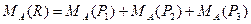 .
.
Учитывая, что 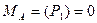 , найдём расстояние АС между линиями действия равнодействующей из выражения:
, найдём расстояние АС между линиями действия равнодействующей из выражения:
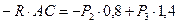 ,
,
откуда
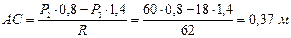 .
.
Дата добавления: 2015-12-26; просмотров: 1624;
