Статическая определимость и статическая неопределимость.
Для рассмотрения равновесия произвольной плоской системы сил статика позволяет составить только три уравнения равновесия, из которых можно определить три неизвестные величины. Если число неизвестных равно числу уравнений равновесия, то такая задача является статически определимой. Если же общее число неизвестных больше числа уравнений равновесия, то такая задача является статически неопределимой. Решить ее методами статики нельзя, так как для этого необходимо рассматривать не абсолютно твёрдые тела, а деформируемые, которые изучают в курсах «Сопротивление материалов» и «Теория упругости». При помощи методов этих наук составляют недостающие уравнения.
8. ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ
В БАЛОЧНЫХ СИСТЕМАХ
Виды опор
Балками называют такие элементы конструкций машин, приборов, сооружений, которые в процессе работы воспринимают в основном поперечные относительно оси нагрузки и передают их через опорные устройства другим элементам конструкции или основанию. Примером могут служить такие детали машин, как валы, оси, рычаги, детали строительных конструкций, фермы мостов и т.п. Любая опора лишает балку одной, двух или трёх степеней свободы. Соответственно различают следующие опоры.
Свободное опирание (рис. 8.1). Эта опора лишает балку одной степени свободы – возможности перемещаться в направлении оси у. Но активные силы должны прижимать балку к опоре, в противном случае опора перестает выполнять своёназначение. Таким образом, реакция 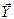 при свободном опирании должна быть направлена всегда только от опоры.
при свободном опирании должна быть направлена всегда только от опоры.




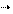
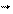
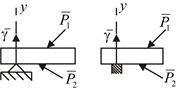
Рис. 8.1. Реакция при свободном опирании балки
Жёсткое опирание – заделка (рис. 8.2). Эта опора лишает балку трёх степеней свободы: линейных перемещений вдоль осей х и у и возможности вращаться. В заделке соответственно появляются три неизвестных реактивных усилия: вертикальная реакция 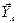 , горизонтальная реакция
, горизонтальная реакция  и реактивный момент заделки МА.
и реактивный момент заделки МА.



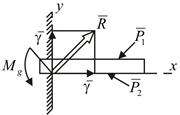
Рис. 8.2
Шарнирно-неподвижная опора препятствует любому поступательному перемещению балки, а также дает возможность последней поворачиваться вокруг оси шарнира (рис. 8.3, а). Реакция приложена в центре шарнира А. Для определения неизвестных модуля и направления реакции 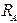 необходимо ее заменить взаимно перпендикулярными составляющими
необходимо ее заменить взаимно перпендикулярными составляющими 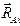 и
и 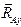 , (
, ( 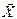 ,
, 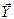 ). На рис. (8.3, б) дано схематическое изображение этой опоры. В качестве примера шарнирно-неподвижной опоры может служить подшипниковый узел (рис. 8.3, в).
). На рис. (8.3, б) дано схематическое изображение этой опоры. В качестве примера шарнирно-неподвижной опоры может служить подшипниковый узел (рис. 8.3, в).



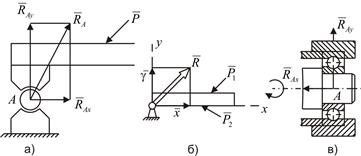
Рис. 8.3
При опирании на шарнирно-подвижную опору нижняя часть поставлена на катки (рис. 8.4, а), поэтому такая опора не препятствует небольшому перемещению балки в направлении, параллельном опорной поверхности. Реакция опоры в данном случае приложена в центре шарнира и направлена по нормали к опорной поверхности (трением катков пренебрегаем). Схематическое изображение дано на рис.8.4, б, в. Примером такой опоры может служить плавающая подшипниковая опора вала.



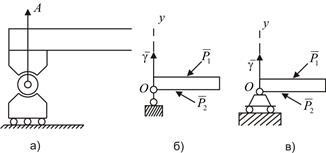
Рис. 8.4
Балки, имеющие опоры, в которых общее число неизвестных реакций равно числу уравнений равновесия, являются статически определимыми.
На рис. 8.5, а, г показаны статически определимые системы (по три реактивных усилия), на рис. 8.5 б, в – статически неопределимые системы (более трех неизвестных реакций).


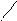




Рис. 8.5
Дата добавления: 2015-12-26; просмотров: 2997;
 при свободном опирании должна быть направлена всегда только от опоры.
при свободном опирании должна быть направлена всегда только от опоры.



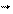

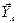 , горизонтальная реакция
, горизонтальная реакция  и реактивный момент заделки МА.
и реактивный момент заделки МА.



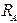 необходимо ее заменить взаимно перпендикулярными составляющими
необходимо ее заменить взаимно перпендикулярными составляющими 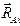 и
и 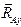 , (
, ( 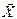 ,
, 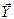 ). На рис. (8.3, б) дано схематическое изображение этой опоры. В качестве примера шарнирно-неподвижной опоры может служить подшипниковый узел (рис. 8.3, в).
). На рис. (8.3, б) дано схематическое изображение этой опоры. В качестве примера шарнирно-неподвижной опоры может служить подшипниковый узел (рис. 8.3, в).