Методические указания к решению задач. При практическом решении задач можно пользоваться любой формой уравнений равновесия, так как они совершенно равноправны

При практическом решении задач можно пользоваться любой формой уравнений равновесия, так как они совершенно равноправны. Изложим некоторые общие правила составления уравнения равновесия.

Оси координат и моментные точки можно выбирать произвольно. Наиболее просто и безошибочно решаются уравнения равновесия, в которые входит одно неизвестное. Следовательно, координатные оси надо направлять перпендикулярно к направлению неизвестных сил. Тогда при составлении уравнений проекций неизвестные, перпендикулярные осям, в эти уравнения не войдут. За моментные целесообразно брать такие точки, в которых пересекаются линии действия двух неизвестных сил. Тогда в уравнение моментов войдёт только одна искомая сила.

Для плоской системы можно выбирать любое число координатных осей и моментных точек и составлять соответствующее число уравнений равновесия, но только три из них будут независимыми. Остальные уравнения являются следствиями этих трех, и их можно использовать лишь для проверки.

Для плоской системы параллельных сил эти общие правила можно конкретизировать. Оси координат следует направлять так, чтобы одна из них оказалась параллельной силам, приложенным к твердому телу. Уравнение моментов нужно составлять относительно точки, лежащей на линии действия неизвестной силы. Это даёт возможность определить одну из неизвестных сил непосредственно из одного уравнения моментов. Для решения задач при помощи двух уравнений моментов следует учитывать, что моментные точки не должны лежать на прямой, параллельной силам.

Задачи на равновесие твердого тела для плоской системы сил рекомендуется решать в следующем порядке.

1. Выделить тело, равновесие которого надо рассмотреть.

2. Изобразить активные (заданные) силы.

3. Освободить тело от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой – число неизвестных величин должно быть не более трёх (для системы параллельных сил не более двух).

4. Направить оси координат и выбрать моментные точки.

5. Составить уравнения равновесия произвольной плоской системы сил (или плоской системы параллельных сил).

6. Решить систему полученных уравнений равновесия относительно неизвестных величин.

Если в результате решения искомая реакция получается положительной, то это значит, что направление её выбрано верно, если отрицательной – направление реакции необходимо заменить на противоположное (модуль её при этом остается прежним).

После того как задача решена, необходимо произвести проверку. Для этого следует составить не применявшуюся при решении сумму моментов или проекций, при этом необходимо учитывать уже исправленные направления реакций. Равенство нулю алгебраической суммы проекций или моментов подтвердит правильность решения задачи.

Пример 10. Определить реакции опор двухконсольной балки, на- груженной силой Р = 400 H (a = 60°), двумя равномерно распределёнными нагрузками интенсивностью 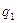= 100 H/м, 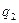= 200 H/м и парой сил с моментом М = 2000 Hм (рис. 8.6, а).

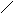
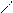
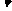
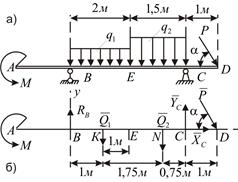
Рис. 8.6

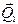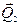Решение. Заменим равномерно распределённые нагрузки сосредоточенными силами и , приложенными в точках К (середина ВЕ) и N (середина СЕ):

, .

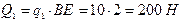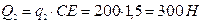Рассмотрим равновесие балки. К ней приложены активные нагрузк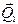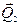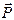и , , и 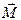. Отбросим связи. Подвижную опору заменяем вертикальной реакцией 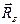, а неподвижную опору С – горизонтальной 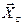и вертикальной 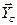(рис .8.6, б). Имеется три неизвестных – задача статически определима. Направим оси координат и составим уравнения равновесия:

, ;

, ;

, .

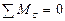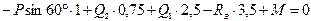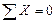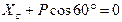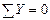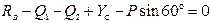Решив полученную систему уравнений, найдём:

, , .

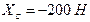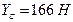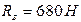Направление горизонтальной реакции в опоре С необходимо изменить на противоположное. Для проверки составим сумму моментов относительно точки Е:

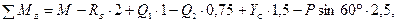
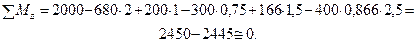
Относительная погрешность результата

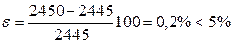вполне допустима.

9. РАВНОВЕСИЕ СИСТЕМ СОЧЛЕНЁННЫХ ТЕЛ

Системой сочленённых тел называют несколько твёрдых тел, касающихся друг друга или соединенных между собой посредством шарниров, стержней, нитей.

При решении задач, в которых рассматривается равновесие системы тел, число неизвестных может превысить число уравнений статики, составленных для всей системы в целом. Кроме того, часто требуется найти силу, с которой одно сочленённое тело действует на другое. Для решения таких задач необходимо рассматривать равновесие каждого тела отдельно, составляя для него соответствующие уравнения равновесия. При этом остальные тела сочленённой системы являются связями, наложенными на рассматриваемое тело.

Метод, основанный на рассмотрении равновесия отдельных частей системы твёрдых тел, называют методом расчленения. Иногда рассматривают также равновесие всей системы тел в целом или группы тел, входящих в систему. При этом к системе тел, представляющих в совокупности нетвёрдое тело, можно применить принцип отвердевания (при затвердевании всякого нетвёрдого тела равновесие не нарушается). В этом случае в уравнения равновесия не войдут силы, с которыми отдельные тела действуют друг на друга.