ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ

10.1. Равнодействующая пространственной
системы сходящихся сил

Любую силу 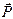можно представить диагональю прямоугольного параллелепипеда, построенного на составляющих 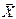, , 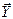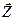(рис. 10.1), которые по модулю равны проекциям данной силы на оси координат х, у, z.Модуль и направление 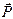определяют по формулам:

,

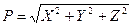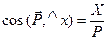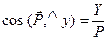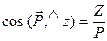, , . (10.1)

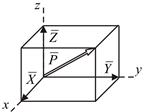
Рис. 10.1

Система сил, линии действия которых не лежат в одной плоскости, но пересекаются в данной точке, называется пространственной системой сходящихся сил.

Равнодействующая пространственной системы сходящихся сил равна геометрической сумме слагаемых сил:

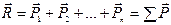. (10.2)

Равнодействующая 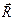выражается замыкающей стороной пространственного силового многоугольника, стороны которого равны и параллельны данным силам. В частности, если число слагаемых сходящихся сил равно трём, то их равнодействующая по модулю и направлению выражается диагональю параллелепипеда, построенного на этих силах. Силовой многоугольник пространственной системы сходящихся сил не является плоской фигурой, поэтому при сложении сходящихся сил, не лежащих в одной плоскости, предпочтительнее аналитический метод.

Воспользуемся теоремой: проекция равнодействующей системы сходящихся сил на какую-либо ось равна сумме проекций всех сил на эту же ось. Найдём проекции равнодействующей 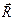на координатные оси:

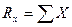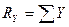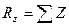, , . (10.3)

Зная составляющие, по формулам (10.1) найдём модуль и направление равнодействующей.