Уравнение равновесия плоской системы сил

Условия равновесия плоской системы сил. Для равновесия плоской системы сил необходимо и достаточно, чтобы главный вектор 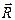и главный момент 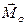этой системы относительно любого произвольно выбранного центра О равнялись нулю, т. е.

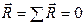, (7.8)

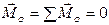. (7.9)

В векторной форме условие (7.8) применять для решения задач неудобно. Спроектировав уравнение (7.8) на оси координат, получим вместе с (7.9) три следующих скалярных равенства:

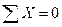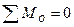; ; . (7.10)

Систему (7.10) называют первой формой уравнений равновесия произвольной плоской системы сил, которая формулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую координатную ось (х, у) и алгебраическая сумма моментов этих сил относительно любой точки О, лежащей в плоскости действия сил, равнялись нулю.

Вторая форма уравнений равновесияформулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно двух произвольных точек А и В и алгебраическая сумма проекций всех сил на какую-либо ось х или у, не перпендикулярную прямой АВ, равнялись нулю, т. е.

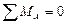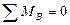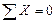; ; (7.11)

или 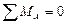; ; 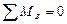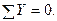(7.12)

Условие неперпендикулярности сил и прямой АВ также обязательно. В противном случае, одно из уравнений системы (7.11) или (7.12) не является независимым.

Третья форма уравнений равновесияформулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно трех произвольных точек А, В и С, не лежащих на одной прямой, равнялись нулю, т. е.

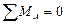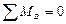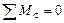; ; . (7.13)

Если бы точки А, В и С лежали на одной прямой, то одно из уравнений не являлось бы независимым (его можно было получить из двух других путем тождественных преобразований). Решение задачи было бы равносильно решению системы двух уравнений с тремя неизвестными, что невыполнимо.

Все три формы уравнений равновесия совершенно равноправны. Отметим, что независимо от вида уравнений равновесия для плоской системы произвольно расположенных сил статика позволяет составить только три уравнения.

Условия равновесия плоской системы параллельных сил.Если силы перпендикулярны какой-либо оси х, то уравнение 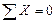превращается в тождество 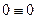. Для определения неизвестных сил остается два уравнения равновесия, которые можно представить в двух формах.

Первая форма. Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма всех сил и алгебраическая сумма моментов всех сил относительно произвольной точки О равнялись нулю, т. е.

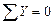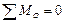; . (7.14)

Вторая форма. Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно двух произвольных точек А и В равнялись нулю, т.е.

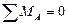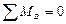; . (7.15)