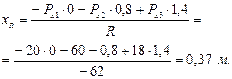Плоская система параллельных сил
Система сил, линии действия которых параллельны и лежат в одной плоскости, называется плоской системой параллельных сил.
Сложение двух параллельных сил. Две параллельные силы 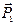 и
и 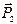 , направленные в одну сторону или в разные стороны, приводятся к одной равнодействующей силе
, направленные в одну сторону или в разные стороны, приводятся к одной равнодействующей силе 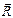 , параллельной этим силам (рис. 7.1).
, параллельной этим силам (рис. 7.1).



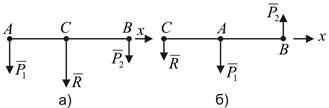
Рис. 7.1
Модуль равнодействующей равен алгебраической сумме (разности) модулей сил 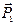 и
и 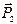 , т.е.
, т.е.
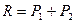 ,
, 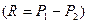 .
.
Знак алгебраической суммы указывает, в какую сторону направлена равнодействующая: «+» – равнодействующая направлена в сторону положительного направления оси проекции, «–» – в противоположном направлении.
Если связать систему параллельных сил с осями координат (рис. 7.2), то
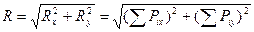 , (7.1)
, (7.1)
т.е. модуль равнодействующей системы параллельных сил равен алгебраической сумме проекций сил системы на ось, параллельную этим силам.



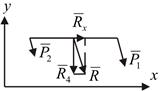
Рис. 7.2
Для системы сил, показанной на рис. 7.1, 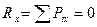 . Следовательно, её модуль равен
. Следовательно, её модуль равен
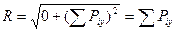 .
.
Линия действия равнодействующей  внутренним (внешним) образом делит расстояние между точками приложения сил на части, обратно пропорциональные модулям сил (рис. 7.1, а, б):
внутренним (внешним) образом делит расстояние между точками приложения сил на части, обратно пропорциональные модулям сил (рис. 7.1, а, б):
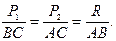 (7.2)
(7.2)
Сложение нескольких параллельных сил. Система нескольких параллельных сил 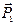 ,
, 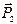 …
… 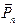 приводится к одной равнодействующей
приводится к одной равнодействующей 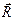 , равной по модулю алгебраической сумме составляющих:
, равной по модулю алгебраической сумме составляющих:
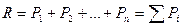 . (7.3)
. (7.3)
Точку приложения равнодействующей системы параллельных сил называют центром параллельных сил. Координаты центра параллельных сил х0 и у0 находят по формулам:
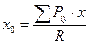 ,
, 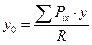 , (7.4)
, (7.4)
где х и у – координаты точек приложения составляющих сил.
Положение центра параллельных сил не зависит от выбора системы координат. Обычно систему координат выбирают так, что силы параллельны какой-либо оси (например, у). Тогда достаточно определить только координату х0 линии действия равнодействующей.
Пример 8. К телу в точках А, В и D приложены параллельные силы 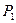 = 20 Н,
= 20 Н, 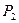 = 60 Н и
= 60 Н и 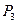 = 18 Н (рис. 7.3). Определить модуль, направление и линию действия равнодействующей.
= 18 Н (рис. 7.3). Определить модуль, направление и линию действия равнодействующей.



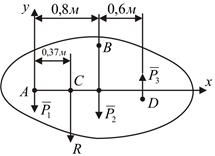
Рис. 7.3
Решение:
1. Приняв точку А за начало координат, направим ось х перпендикулярно данным силам, а ось у – параллельно им.
2. Найдём модуль равнодействующей:
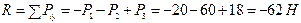 .
.
Так как знак алгебраической суммы проекций получился отрицательным, то вектор равнодействующей направлен вниз, в сторону отрицательного направления оси y.
3. Определим положение равнодействующей:
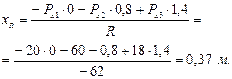
Дата добавления: 2015-12-26; просмотров: 3278;
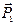 и
и 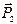 , направленные в одну сторону или в разные стороны, приводятся к одной равнодействующей силе
, направленные в одну сторону или в разные стороны, приводятся к одной равнодействующей силе 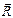 , параллельной этим силам (рис. 7.1).
, параллельной этим силам (рис. 7.1).




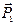 и
и 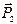 , т.е.
, т.е.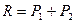 ,
, 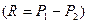 .
.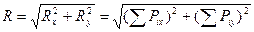 , (7.1)
, (7.1)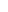




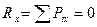 . Следовательно, её модуль равен
. Следовательно, её модуль равен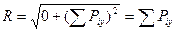 .
.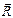 внутренним (внешним) образом делит расстояние между точками приложения сил на части, обратно пропорциональные модулям сил (рис. 7.1, а, б):
внутренним (внешним) образом делит расстояние между точками приложения сил на части, обратно пропорциональные модулям сил (рис. 7.1, а, б):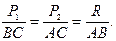 (7.2)
(7.2)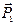 ,
,  …
… 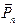 приводится к одной равнодействующей
приводится к одной равнодействующей 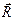 , равной по модулю алгебраической сумме составляющих:
, равной по модулю алгебраической сумме составляющих: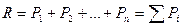 . (7.3)
. (7.3)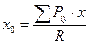 ,
, 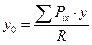 , (7.4)
, (7.4) = 20 Н,
= 20 Н,  = 60 Н и
= 60 Н и  = 18 Н (рис. 7.3). Определить модуль, направление и линию действия равнодействующей.
= 18 Н (рис. 7.3). Определить модуль, направление и линию действия равнодействующей.



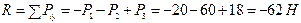 .
.