Статическая определимость кинематической цепи

При силовом анализе механизмов (определении неизвестных сил, действующих на движущиеся звенья) можно использовать уравнения (законы) статики. Докажем это положение, проанализировав реакции в кинематических парах (табл.).

Кинематические пары	Равновесие каждого звена	Известные параметры	Неизвестные параметры
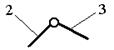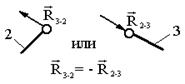
5-й класс Вращательная		Точка приложения	Величина, направление
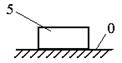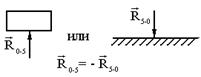
Поступательная		Направление	Величина, точка приложения
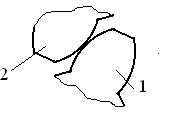
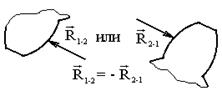
4-й класс		Точка приложения, направление	Величина

Примечание. 2, 3, 5 – номера звеньев.

В кинематических парах 5-го класса известно по одному параметру сил реакций, неизвестны два, в кинематических парах 4-го класса известны два параметра, а неизвестен один.

Таким образом, плоская кинематическая цепь, состоящая из кинематических пар 5-го и 4-го классов, имеет 2Р₅ + Р₄ неизвестных величин сил реакций.

В то же время для одного звена можно составить 3 уравнения статики, а для nзвеньев – 3n уравнений статики.

Кинематическая цепь будет статически определима, если число неизвестных величин сил реакций не превышает числа возможных уравнений статики, т.е.

3n = 2P₅ + Р₄.

Это и есть условие статической определимости кинематической цепи.

Полученное равенство можно записать в виде

3n – 2Р₅ – Р₄ = 0.

Но запись слева от знака равенства является числом степеней свободы кинематической цепи W, т.е.

W = 3n – 2Р₅ – P₄ = 0.

Как известно (см. раздел 1 «Структура и классификация механизмов»), таким свойством (W=0) обладают структурные группы, или группы Асура – статически определимые кинематические цепи.

Метод силового анализа, приведенный ниже, называется кинетостатическим, так как для определения сил реакций в кинематических парах, возникающих при движении звеньев, используются уравнения статики.

Порядок (последовательность) силового анализа рычажного механизма:

1. Выделяем из механизма последнюю (крайнюю, наиболее удаленную от ведущего звена) структурную группу и проводим её силовой расчёт, используя уравнения статики.

2. Выделяем из механизма следующую структурную группу и проводим её силовой расчёт.

3. Силовой расчёт заканчиваем силовым расчётом ведущего звена.

Пример

Задан шестизвенный рычажный механизм (рис. 3.4), состоящий из начального механизма (звенья 0 и 1) и структурных групп, образованных звеньями 2 и 3 (двухповодковая структурная группа 2-го класса, 1-го вида) и 4, 5 (структурная группа 2-го класса, 2-го вида).

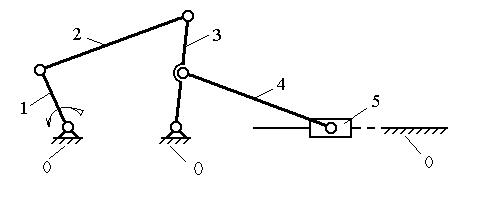
Рис. 3.4. Шестизвенный рычажный механизм

Решение

1. Проводим силовой расчёт структурной группы 4-5 (определяем неизвестные реакции, если известны внешние силы, действующие на звенья 4 и 5):

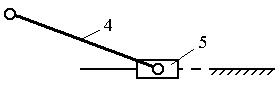
2. Проводим силовой расчёт структурной группы 2-3:

3. Проводим силовой расчёт ведущего звена: