Геометрическая вероятность
Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости и т.д.). Применяется для расчета вероятностей, если проводимые испытания имеют бесконечное число элементарных исходов.
Пусть отрезок l составляет часть отрезка L . На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно L , т.е.
P = Длина l / Длина L (1.9)
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит от ее расположения относительно G , т.е.
P = площадь g / площадь G (1.10)
Формулы (1.9), (1.10) определяют геометрическую вероятность. Аналогичную формулу можно получить и для трехмерного пространства.
Пример. Два лица А и В условились встретиться в определенном месте между 12 часами и часом. Пришедший первым ждет другого в течении 20 минут, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них в течении установленного часа может произойти наудачу и моменты прихода независимы.
Решение. Обозначим моменты прихода лица А через x и лица В через y . Для того, чтобы встреча произошла, должно выполниться условие 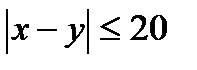 . Изобразим x и y как координаты точки плоскости. В качестве единицы масштаба выберем минуту.
. Изобразим x и y как координаты точки плоскости. В качестве единицы масштаба выберем минуту.
Возможные исходы изобразятся точками квадрата со сторонами 60, а благоприятствующие встрече исходы расположатся в заштрихованной области.
Искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата
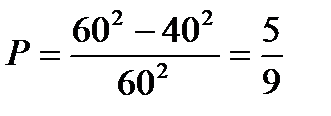
| y |
| x |
Дата добавления: 2015-12-26; просмотров: 690;
