Классическое определение вероятности

Основные понятия теории вероятностей

Испытание (опыт, эксперимент) – реализация определенного комплекса условий, который может быть повторен неограниченное число раз. При этом комплекс условий включает в себя случайные факторы, реализация которых в каждом испытании приводит к неоднозначности исхода испытания.

Пример:

1. Подбрасывание монеты.

2. Стрельба по некоторой цели.

Событие – всякий факт, который в результате опыта может произойти или не произойти, или другими словами – это результат опыта независимо от его значения.

Пример.

1. При подбрасывании монеты событием может быть выпадение «герба», выпадение «решки».

2. При стрельбе по некоторой цели событием может быть поражение цели, промах, поражение определенного сектора цели.

События относительно их появления подразделяется на три группы:

1) достоверные;

2) невозможные;

3) случайные.

Достоверное событие – событие, которое всегда произойдет в результате испытания.

Пример.

1. При подбрасывании монеты выпадение «герба» или «решки» есть событие достоверное.

2. При наблюдении за состоянием воды в сосуде при нормальном атмосферном давлении и температуре 200С событие «вода в сосуде находиться в жидком состоянии» есть событие достоверное.

Невозможное событие – событие, которое никогда не произойдет в результате испытания.

Пример.

1. При подбрасывании монеты выпадение «герба» и «решки» является событиями невозможным.

2. При наблюдении за состоянием воды при нормальном атмосферном давлении и температуре 200С событие «вода в сосуде находится в твердом состоянии» является событием невозможным.

Случайное событие – событие, которое в результате испытания может произойти или не произойти, либо при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Пример.

1. При бросании игральной кости выпадение 6-ти очков есть событие случайное.

2. При стрельбе по цели поражение цели, попадание в определенный сектор цели являются случайными событиями.

События как объекты исследования разделяются на две группы:

1) простые;

2) сложные.

Простое событие (элементарный исход) – один из возможных результатов опыта, исключающий появление других результатов. Другими словами простое событие – это результат одного и только одного опыта.

Пример.

1. При подбрасывании одной монеты выпадение «герба» - простое событие.

2. При одновременном подбрасывании двух монет выпадение двух «гербов», выпадение двух «решек» являются простыми событиями.

Сложное событие – событие, которое можно разложить на простые события. Другими словами сложное событие – это комбинация простых событий с помощью логических операций.

Пример.

1. При подбрасывании одной монеты выпадение «герба» или «цифры», а также выпадение «герба» и «цифры» есть сложные события.

2. При одновременном подбрасывании двух монет выпадение «герба» на любой из монет – это сложное событие.

События по отношению друг к другу подразделяются на :

1) несовместные;

2) совместные;

3) равновозможные;

4) образующие полную группу;

5) противоположные.

События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Пример.

1. Выпадение «герба», выпадение «цифры» - несовместные события.

2. Попадание и промах при одном выстреле – несовместные события.

3. Ни одного попадания, одно попадание, два попадания – несовместные события при двух выстрелах по мишени.

События называются совместными, если появление одного события не исключает появления других событий в данном испытании.

Пример.

1. Два спортсмена стреляют один раз. События «попадание первого спортсмена» и «попадание второго спортсмена» - совместные.

2. При одновременном подбрасывании монеты и игральной кости события «выпадения 2-х очков» и «выпадение герба» являются совместными.

События в данном опыте называются равновозможными, если ни одно из них не является более возможным чем другое.

Пример.

1. Выпадение «герба», выпадение «цифры» при бросании монеты один раз.

2. Появление 1, 2, 3, 4, 5, 6 очков при однократном бросании игральной кости.

3. Появление карты бубновой, червовой, трефовой, пиковой масти при вынимании карты из колоды.

Несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу попарно несовместны, то в результате испытания появится одно и только одно из этих событий.

Пример.

1. Выпадение «герба», выпадение «цифры» при бросании монеты образуют

полную группу событий.

2. Попадание, промах при выстреле – полная группа событий.

3. Хотя бы одно попадание, хотя бы один промах при выстрелах - полная группа событий.

4. Появление не менее 3-х очков, появление не более 4-х очков при бросании игральной кости образуют полную группу событий.

Противоположными называются два несовместных события, образующих полную группу. Иногда говорят, событие называется противоположным событию , если оно состоит в не появлении события.

Пример.

1. Безотказная работа всех элементов технической системы, отказ хотя бы одного элемента – противоположные события.

2. Обнаружение не менее двух бракованных изделий в контрольной партии, обнаружение не более одного бракованного изделия – противоположные события.

Вероятность

Вероятность события – это численная мера степени возможности этого события.

Вероятность события A обозначается P(A) .

Свойства вероятности:

1. Вероятность достоверного события равна 1.

2. Вероятность невозможного события равна 0.

3. Вероятность случайного события есть положительное число между 0 и 1.

0 < P(A) < 1,

где A - случайное событие.

4. Вероятность любого события удовлетворяет двойному неравенству

,

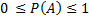где A - любое событие.

Классическое определение вероятности

Вероятностью события A называют отношение числа элементарных исходов, в которых событие A наступает, т.e. благоприятствующих событию A исходов, к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу

P(A) = m/n,

где m - число благоприятствующих событию A исходов, n- число всех равновозможных несовместных элементарных исходов, образующих полную группу.

Пример. 1.В урне находится 7 белых, 2 зеленых и 6 красных шаров. Наудачу вынимается один шар. Найти вероятность того, что извлеченный шар окажется белым (зеленым, красным).

Решение.

-A -извлечение белого шара:

P (A) = m / n

m=7, n = 7+2+6=15

P (A) = 7/15

-B - извлечение зеленого шара:

P (B) = m / n

m=2, n = 7+2+6=15

P (B) = 2/15

-C- извлечение зеленого шара:

P (C) = m / n

m=6, n = 7+2+6=15

P (A) = 6/15 = 2/5

Пример 2. Куб, все грани которого окрашены, распилен на 1000 частей. Найти вероятность того, что у случайно взятого кубика будет окрашена одна грань (две грани, три грани).

Решение.

-A-извлечение кубика с тремя окрашенными гранями:

P (A) = m / n

n = 1000, m = 8, т.к. три окрашенные грани могут быть только у угловых кубиков.

P (A) = 8/1000

-B- извлечение кубика с двумя окрашенными гранями:

P (B) = m / n

n = 1000, m = 12*(10-12) = 12*8 = 96, т.к. две окрашенные грани могут быть у кубиков, находящихся на ребре куба, кроме углов и для получения 1000 кубиков каждое ребро разделено на 10 частей.

P (B) = 96/1000

-C- извлечение кубика с одной окрашенной гранью:

P (C) = m / n

n = 1000, m = 6*(10-2)*(10-2) = 6*8*8 = 384, т.к. одна окрашенная грань окажется у кубиков на гранях (кроме ребер)

P (C) = 384/1000