Основные формулы и правила комбинаторики

Комбинаторика – раздел элементарной математики, в котором изучают количества комбинаций, подчиненных определенным условиям и составляемых из конечного набора элементов (множества) безразлично какой природы.

Формулы и правила комбинаторики используют при непосредственном вычислении вероятностей (по формуле P (A) = m / n ).

Перестановки – комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только их порядком.

Количество перестановок без повторений B_n = n! (1.2)

Пример 1.

1.Сколько трехзначных чисел можно образовать из цифр 1, 2, 3, если каждая цифра в числе содержится один раз?

Решение

n = 3 - количество цифр

B_n = 3! = 1*2*3 = 6

123, 132, 213, 231, 321, 312.

Пример 2.

2.Сколько четырехзначных чисел можно образовать из цифр 0, 1, 2, 3 не повторяя их?

Решение.

n = 4 (1,2,3,0)

B₄ = 4! = 1*2*3*4 = 24

Учитывая, что число с нулем на первом месте является трехзначным, подсчитаем количество таких цифр:

n = 3 (1,2,3,)

B₃ = 3! = 1*2*3 = 6

Тогда k = A₄ – A₃ = 24-6 = 18

Размещения – комбинации, составленные из n различных элементов, взятых по m элементов, которые отличаются либо составом элементов, либо их порядком.

Число размещений без повторений: A^m_n = 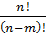(1.3)

Формулы (1.3) и (1.2) связаны между собой формулой A^m_n = B_n при m = n.

Число размещений с повторениями D^m_n = n^m

Пример. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, если цифры в числе могут повторяться?

Решение:

n=3

m=2

D²₃ = 3² = 9

11, 12, 13, 21, 22, 23, 31, 32, 33.

Сочетания – комбинации, составленные из n различных элементов, взятых по m элементов, которые отличаются хотя бы одним элементом.

Число возможных сочетаний без повторений 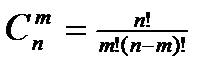(1.5)

Пример. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, если цифры в числе не повторяются?

Решение:

n=3

m=2

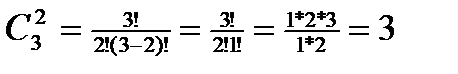
12, 13, 23.

Формулы (1.2), (1.3) и (1.5) связаны между собой следующей формулой 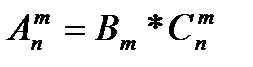(1.6)