Теорема о вероятности появления хотя бы одного события
Вероятность появления хотя бы одного из событий A1, A2,…, An, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 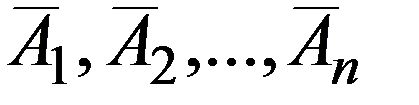 .
.
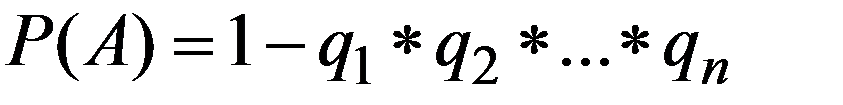 (2.18)
(2.18)
Если события A1, A2,…, An имеют одинаковую вероятность, равную p, то вероятность появления хотя бы одного из этих событий
P (A) = 1 – qn (2.19)
Пример. Сообщение, передаваемое по каналу связи, состоит из n знаков. При передаче каждый знак искажается независимо от других с вероятностью p. Для надежности сообщение дублируется (повторяется) k раз. Найти вероятность того, что хотя бы одно из переданных сообщений не будет искажено ни в одном знаке и количество раз передачи сообщений, чтобы вероятность хотя бы одного неискаженного сообщения стала не меньше P.
Решение.
Вероятность того, что символ не будет искажен (1-p);
вероятность того, что одно сообщение не будет искажено (1-p)n , будет искажено 1-(1-p)n (по (2.19);
вероятность того, что все k сообщения будут искажены (1-(1-p)n)k;
вероятность того, что хотя бы одно из k сообщений не будет искажено по (2.19) 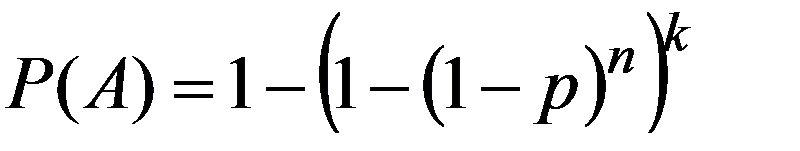
Для определения значения k решим неравенство
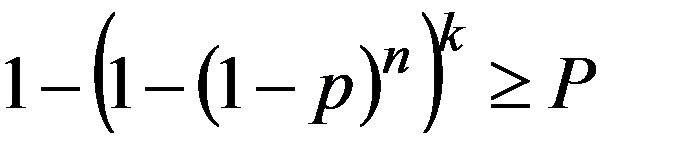
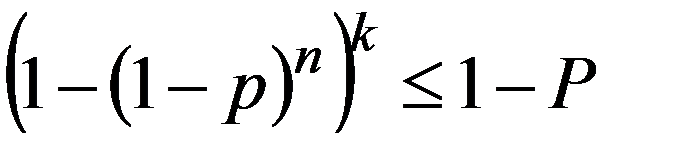

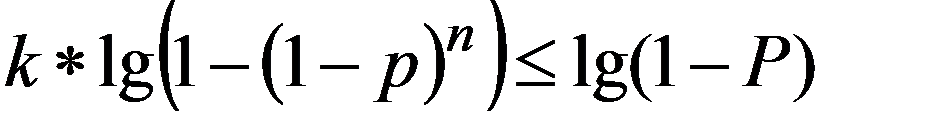
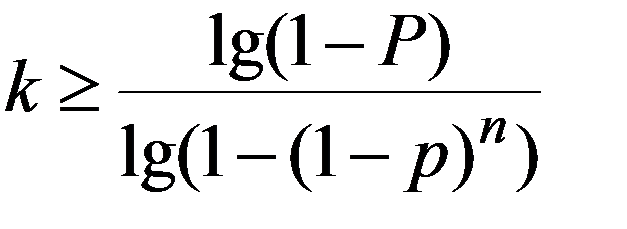
Дата добавления: 2015-12-26; просмотров: 1115;
