Формула полной вероятности
Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий H1, H2,…, Hn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A
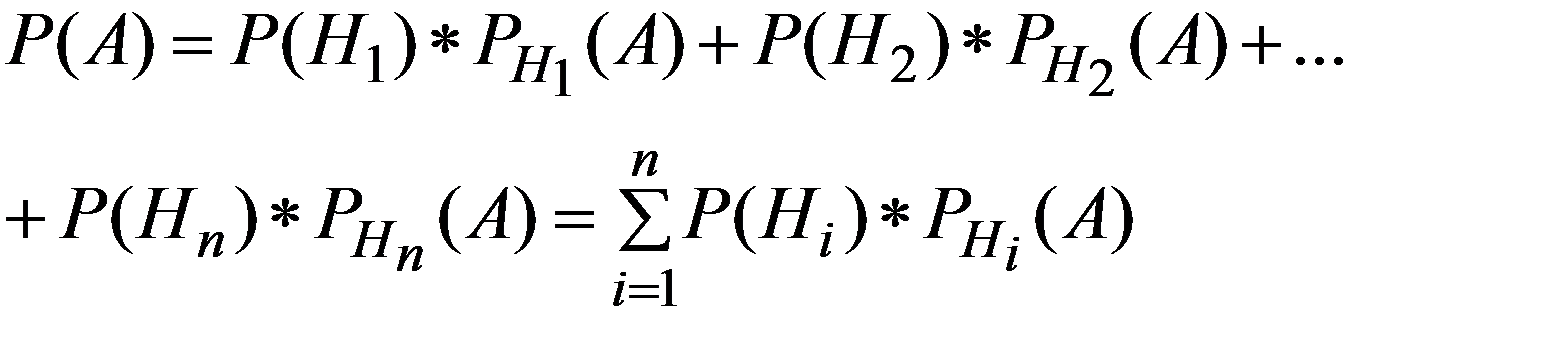 (2.20)
(2.20)
События H1, H2,…, Hn называются гипотезами.
Пример1. Имеются две корзины: в первой a белых шаров и b черных; во второй c белых и d черных. Из первой корзины во вторую перекладывают не глядя один шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
Решение.
Событие A - появление белого шара из второй корзины
Гипотезы H1 - переложен из первой корзины во вторую белый шар,
H2 - переложен черный шар.

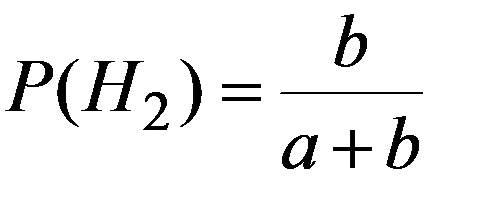


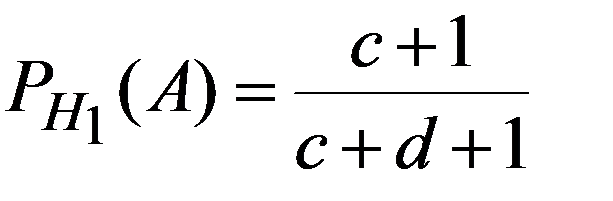
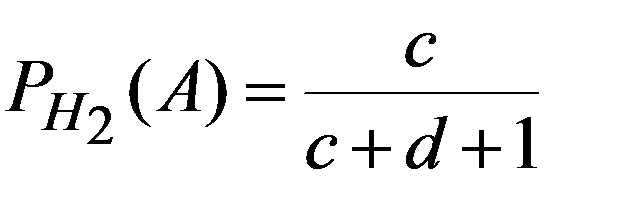
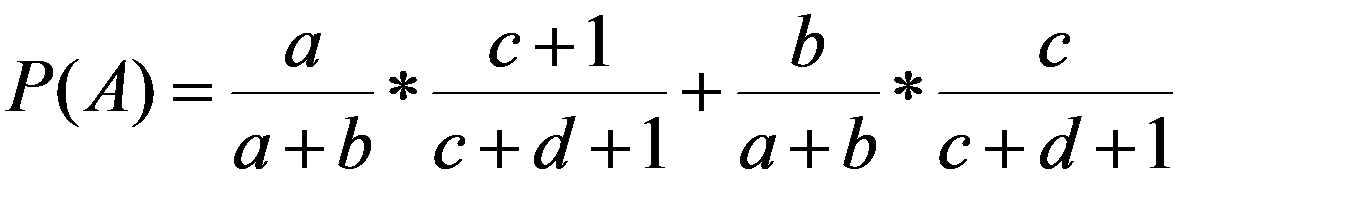
Пример 2. Имеются три одинаковые корзины. В первой a белых шаров и b черных; во второй c белых и d черных, в третьей только белые шары. Некто подходит наугад к одной из корзин и вынимает из нее один шар. Найти вероятность того, что этот шар белый.
Решение.
Событие A - появление белого шара
Гипотезы H1 - выбор первой урны,
H2 - выбор второй урны,
H3 - выбор третьей урны.
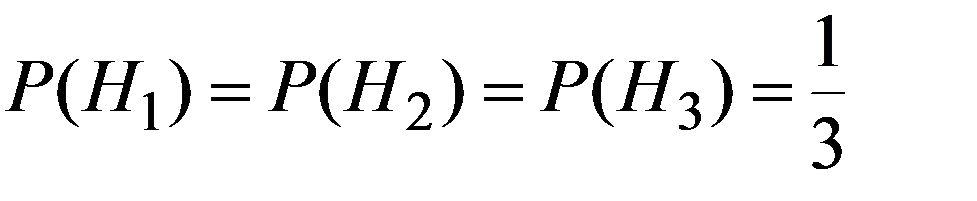
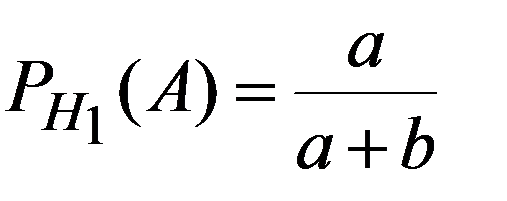
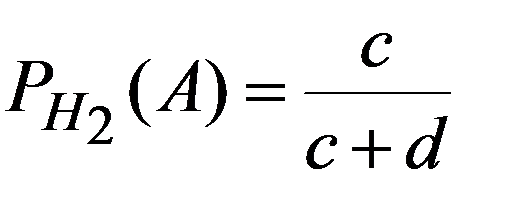
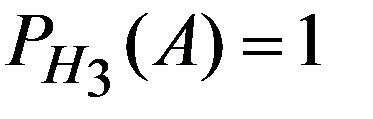
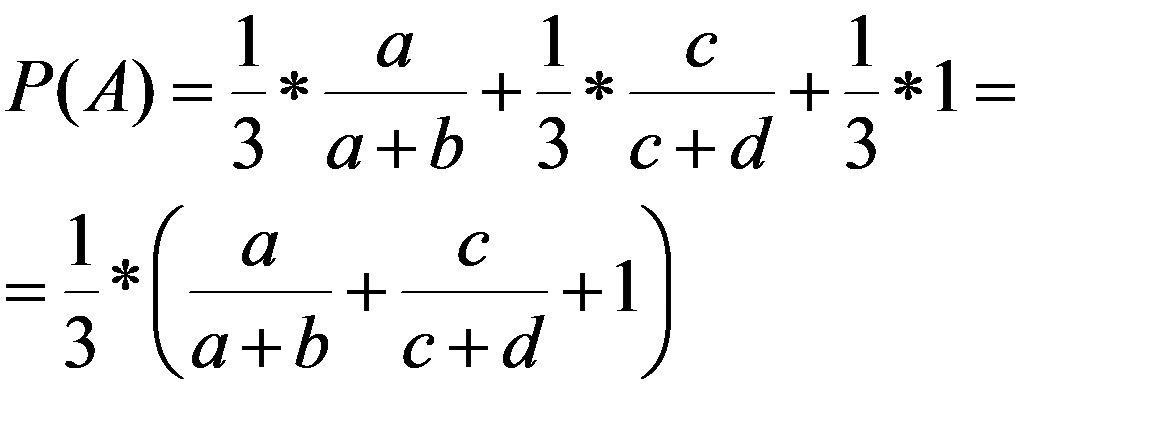
Формула Бейеса (теорема гипотез)
Если до опыта вероятности гипотез H1, H2,…, Hn были равны соответственно P(H1), P(H2),…, P(Hn) , а в результате опыта произошло событие A , то новые (условные) вероятности гипотез вычисляются по формуле
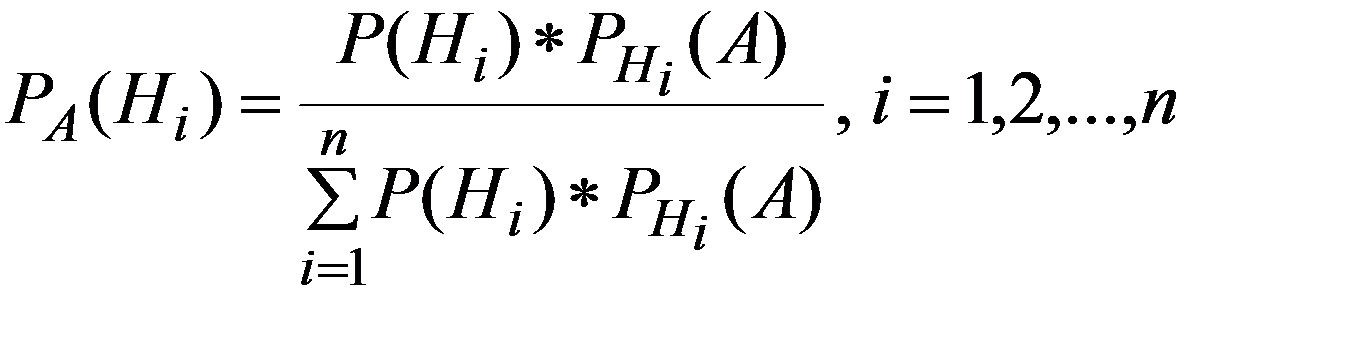
Вероятности P(Hi) называются априорными (доопытными), (2.21)
Вероятности PA(Hi) - апостериорными (послеопытными).
Формула Бейеса (2.21) дает возможность «пересмотреть» возможности (переоценить вероятности) гипотез с учетом результата испытания.
Пример. По каналу связи, на который могут действовать помехи, передается одна из двух кодовых комбинаций 111 или 000 с вероятностями 0,8 и 0,2 соответственно. Через помехи вероятность верного получения каждого из символов комбинации равна 0,6. Считается, что символы кодовых комбинаций искажаются независимо друг от друга. Определить, какая кодовая комбинация была отправлена, если получена – 000.
Решение.
Гипотезы H1 - отправлена комбинация 111
H2 - 000
P(H1) = 0,8, P(H2) = 0,2
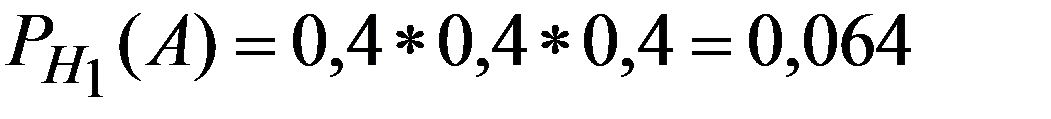
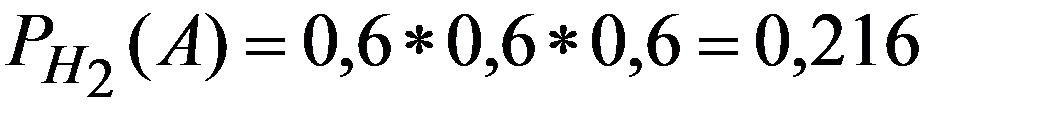
По (2.20) 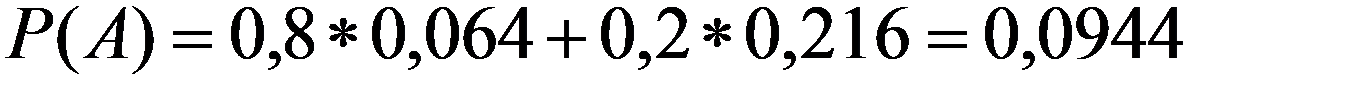
По (2.21) 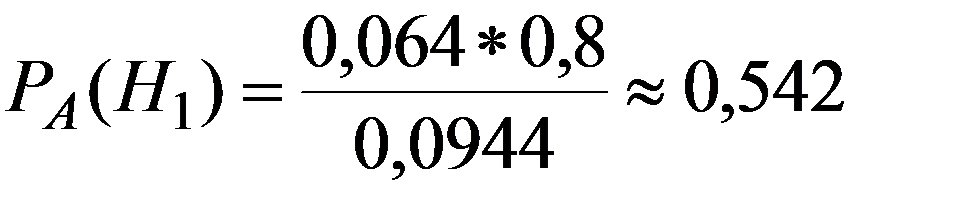
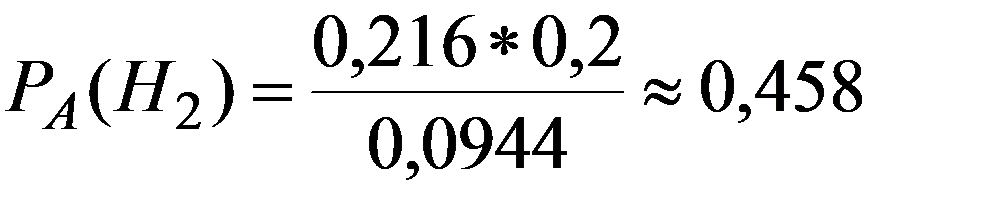
Сравнив PA(H1) и PA(H2) делаем вывод, что при полученной комбинации 000 вероятнее была отправлена комбинация 111.
Формула Бернулли.
Если производится n независимых опытов, в каждом из которых событие A появляется с вероятностью q , то вероятность того, что событие A произойдет в этих n опытах ровно k раз, выражается формулой Бернулли
. 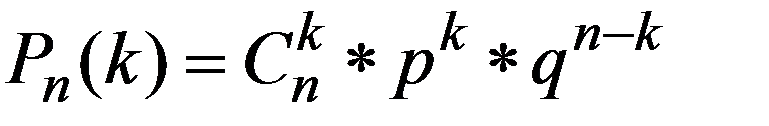 , 0≤ k ≤ n (2.22)
, 0≤ k ≤ n (2.22)
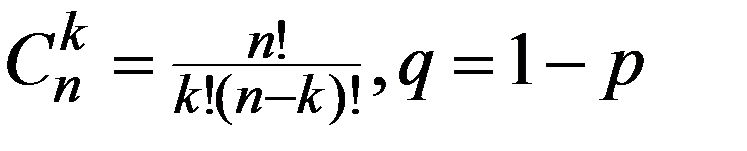
Формула (2.22) выражает так называемое биномиальное распределение вероятностей и применяется, как правило, при n ≤ 10
Пример. Сообщение передается серией кодированных сигналов. В серии из десяти сигналов, вероятность получения каждого сигнала p=0,2. Сообщение считается принятым, если из серии получено четыре сигнала. Какова вероятность принять переданное сообщение.
Решение.
Событие A - сигнал принят, n=10, k=4.
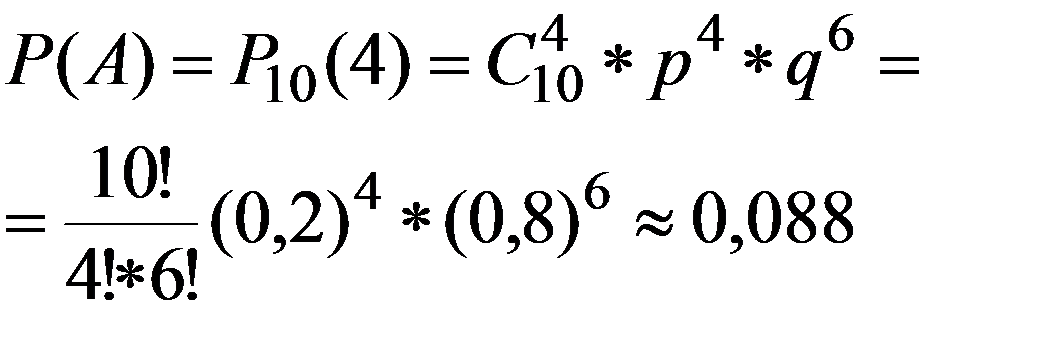
Значение k , при котором Pn(k) превышает или, по крайней мере, не меньше, вероятности остальных возможных исходов испытания называют наивероятнейшим, обозначают k0 и определяют из двойного неравенства
(np – q) ≤ k0 ≤ (np + p) (2.23)
При этом, если
(np – q) - дробное, то существует одно наивероятнейшее число k0 ;
(np – q) - целое, то существует два наивероятнейших числа: k0 и k0 + 1;
(np) - целое, то k0 = n*p .
Пример. Вероятность того, что в течении одного дня на предприятии будет перерасход воды равна 0,3 . Определить наиболее вероятное число дней в течении месяца (30-ти дней) с нормальным расходом воды.
Решение.
n=30 , p = 1-0,3 = 0,7; q=0,3
По (2.23) 30*0,7 – 0,3 ≤ k0 ≤ 30*0,7 + 0,7
20,7 ≤ k0 ≤ 21,7
k0 = 21
Формула Пуассона
Если число n независимых испытаний достаточно велико (n ≥ 100) , а вероятность p появления события A в каждом испытании постоянна и мала (p ≤ 0,1) , и n*p ≤ 10, то вместо (2.22) используют асимптотическую формулу Пуассона
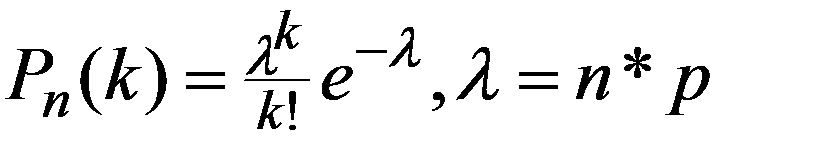 (2.24)
(2.24)
Пример. Радиоприбор состоит из 1000 элементов, которые работают независимо друг от друга. Каждый из них может выйти из строя с вероятностью 0,002. Вычислить вероятность того, что во время работы прибора из строя выйдут от 3 до 6 элементов.
Решение.
n = 1000, p = 0,002, n*p = 2
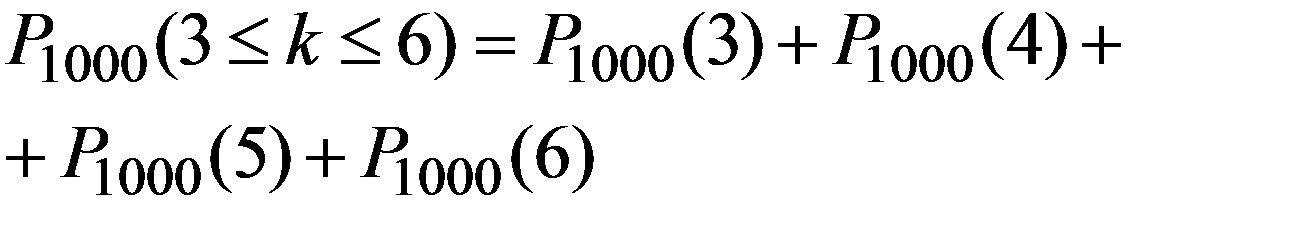
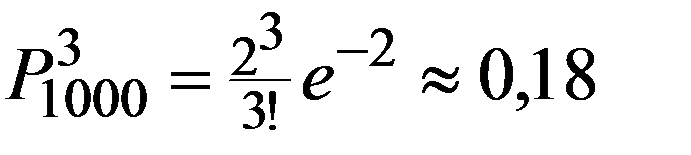
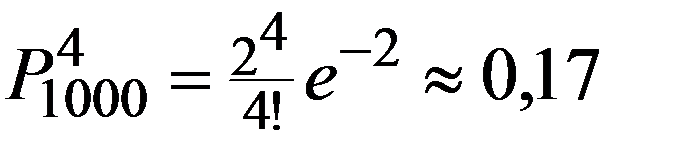
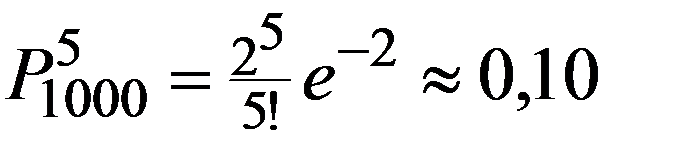
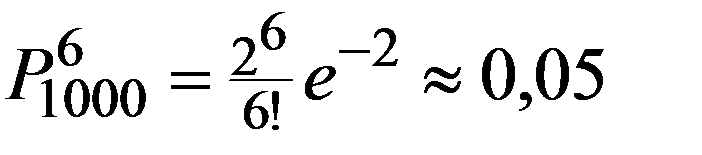
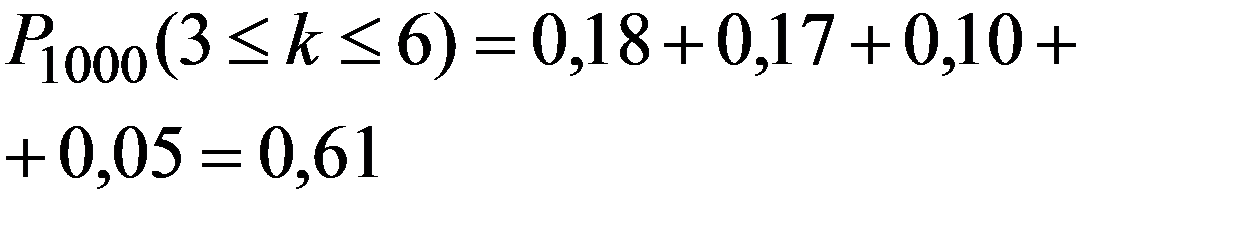
Локальная формула Лапласа.
Если число n независимых испытаний достаточно велико, а вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, а так же n*p > 10 , то вместо (2.22) используют асимптотическую локальную формулу Лапласа
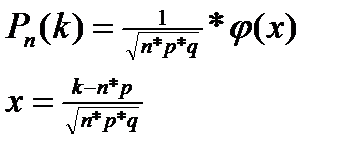 (2.25)
(2.25)
p ≠ 0, p ≠ 1
Функция 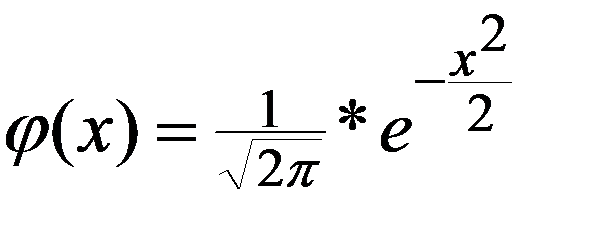 называется функцией Гаусса и имеет свойства:
называется функцией Гаусса и имеет свойства:
- четности 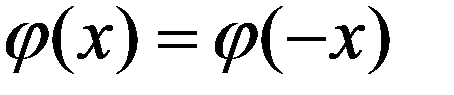 ;
;
- если x > 4, то 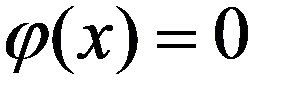 ;
;
- протабулирована на отрезке [0;4] .
Пример. В партии резисторов 75% изделий не имеют дефектов. Из партии случайным образом отбирают 400 резисторов. Вычислить вероятность того, что 290 штук среди отобранных не будет иметь дефектов.
Решение.
n = 400, k = 290, p = 0,75, q = 0,25
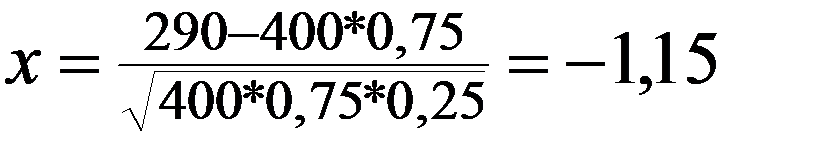
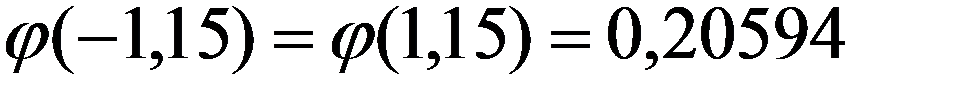

Дата добавления: 2015-12-26; просмотров: 1048;
