Формы представления закона распределения НСВ.

Ряд распределения, многоугольник распределения и формула не используются в качестве закона распределения НСВ.

Функция распределения НСВ X , есть непрерывная, кусочно-дифференцируема функция с непрерывной производной.

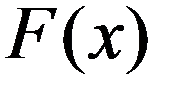
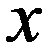
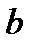
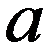
График функции распределения НСВ X, которая принимает все возможные значения на интервале (a,b) .

Из свойства 2 функции распределения вытекает важное следствие для НСВ: вероятность того, что НСВ примет одно определенное значение равна 0. И тогда

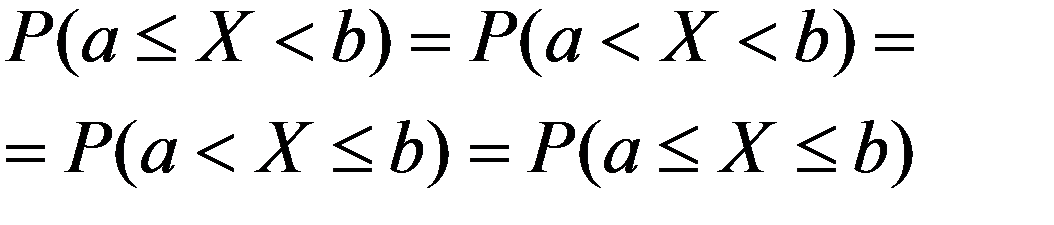
Таким образом, не представляет интереса говорить о вероятности того, что НСВ примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малой.

При этом надо понимать, что 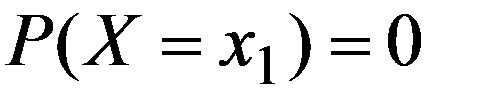не означает, что событие X = x₁ невозможно. В результате испытания НСВ обязательно примет одно из возможных значений, в том числе и x₁ .

Плотность вероятностей (плотность распределения вероятностей, плотность) НСВ X f(x) - функция, определяемая как первая производная функции распределения F(x)

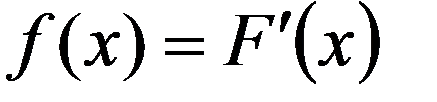(3.7)

Из определения следует, что F(x) - есть первообразная f(x) и выражается через f(x) формулой

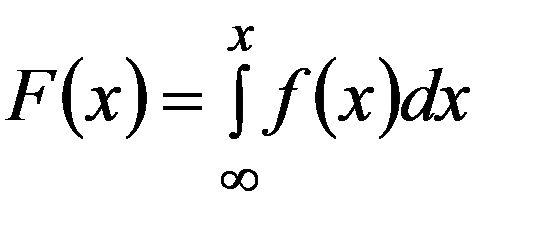(3.8)

Геометрически F(x) есть площадь кривой распределения, лежащая левее точки x.

График f(x) называется кривой распределения.

Размерность f(x) обратна размерности СВ (это не вероятность).

Свойства f(x) :

1. f(x) неотрицательная функция, т.е. f(x) ≥ 0

2.Несобственный интеграл от f(x) на интервале (-∞; +∞) равен 1.

(3.9)

Это так называемое условие нормировки плотности распределения.

Если все возможные значения НСВ X принадлежат интервалу (a,b) , то

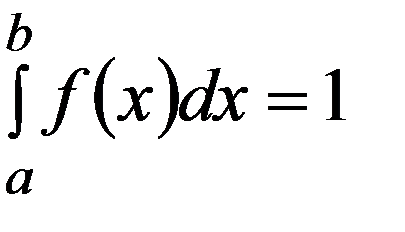(3.10)

3.Вероятность того, что НСВ X примет значение из интервала (a,b) равна определенному интегралу от f(x) , взятому на интервале (a,b)

(3.11)

Геометрически это означает, что P (a < X < b) есть площадь под кривой распределения, ограниченная линиями x=a и x=b слева и справа соответственно и осью абсцисс внизу.

Величина f(x)dx для НСВ называется элементом вероятности и приближенно равна вероятности попадания СВ X на элементарный отрезок 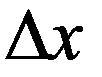, примыкающий к точке x .

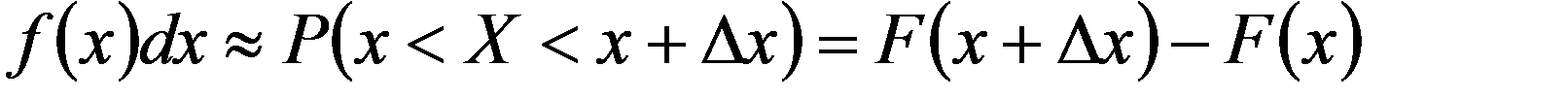(3.12)

Пример. Для НСВ X, плотность распределения которой имеет вид

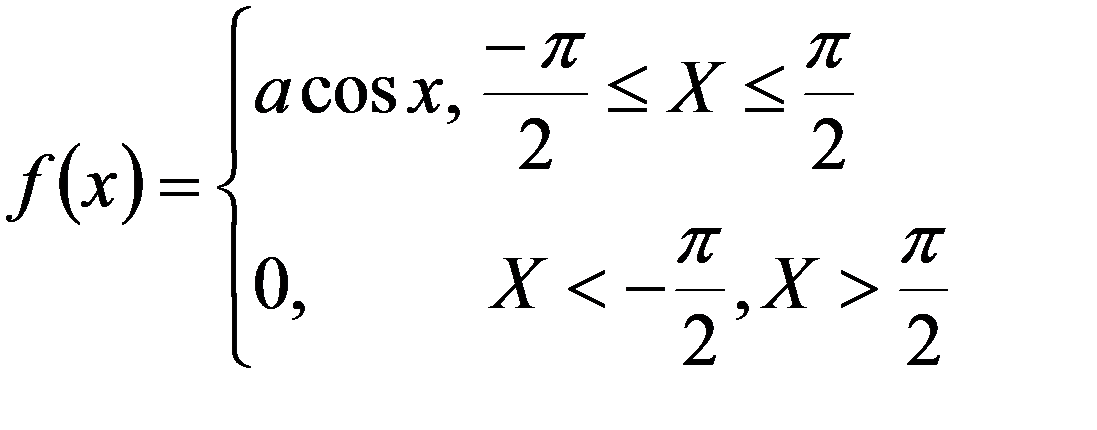
1) Определить коэффициент a ;

2) Построить кривую распределения;

3) Найти F(x) и построить её график;

4) Вычислить P ( 0 < X < π/4)

Решение:

1. По (3.9)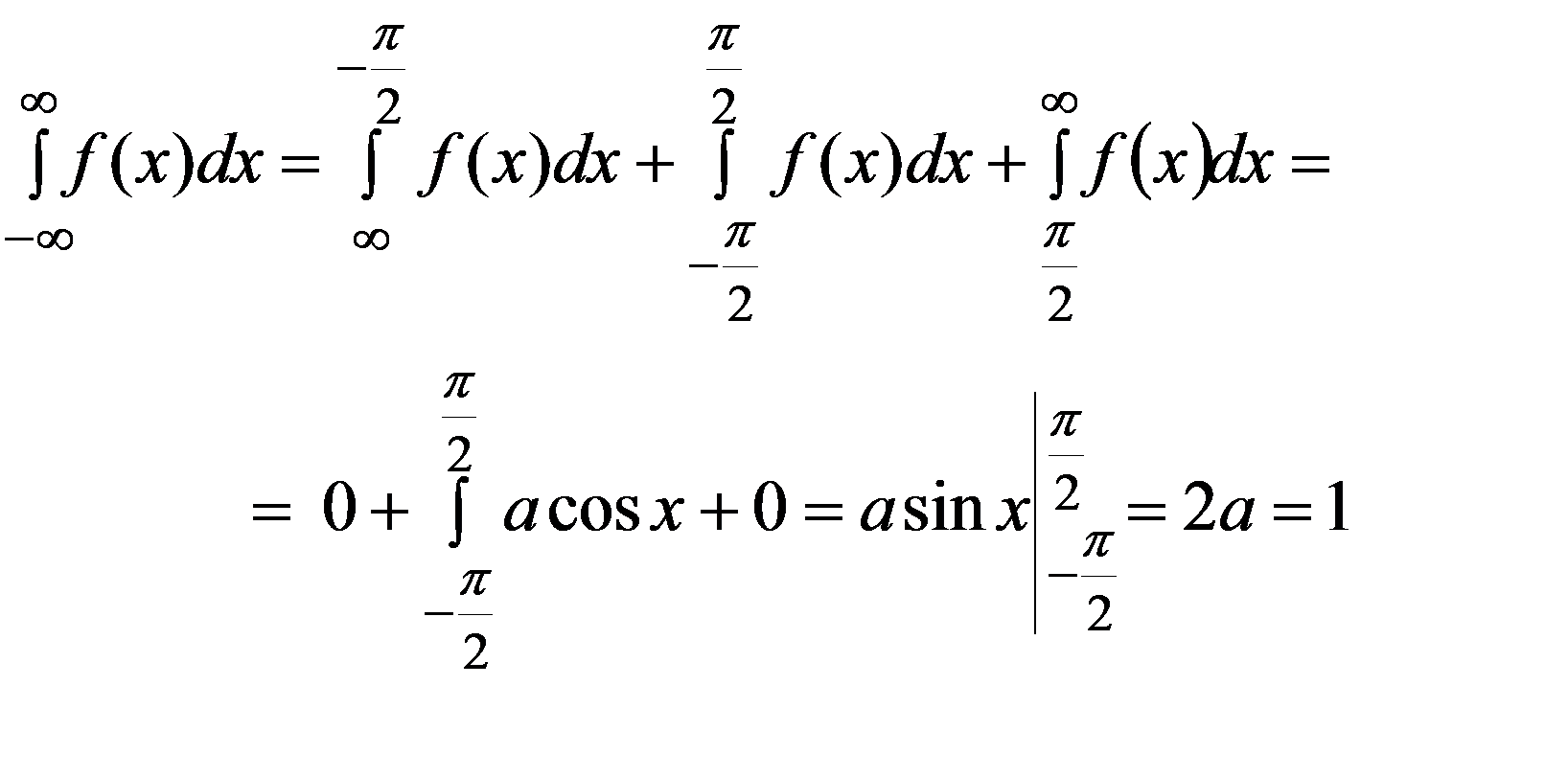

a = ½

2. Кривая распределения f(x)

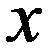
3. По (3.8)

При x < - π/2

При - π/2 ≤ x ≤ π/2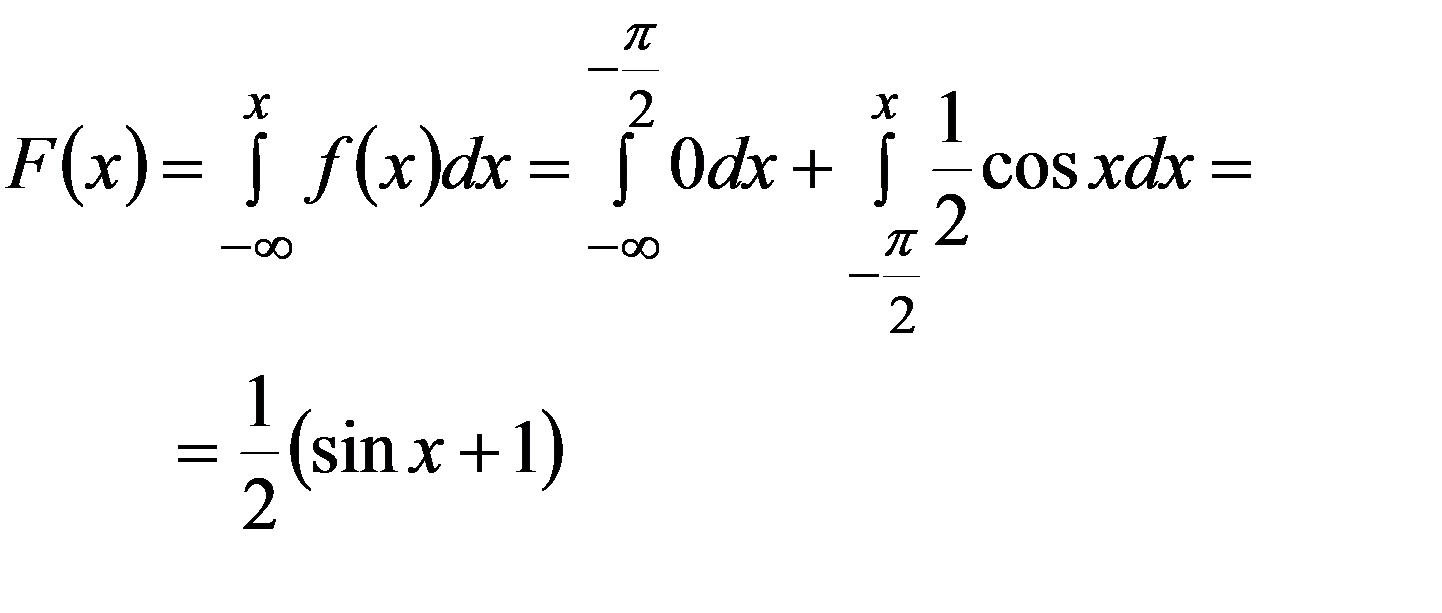

При x > π/2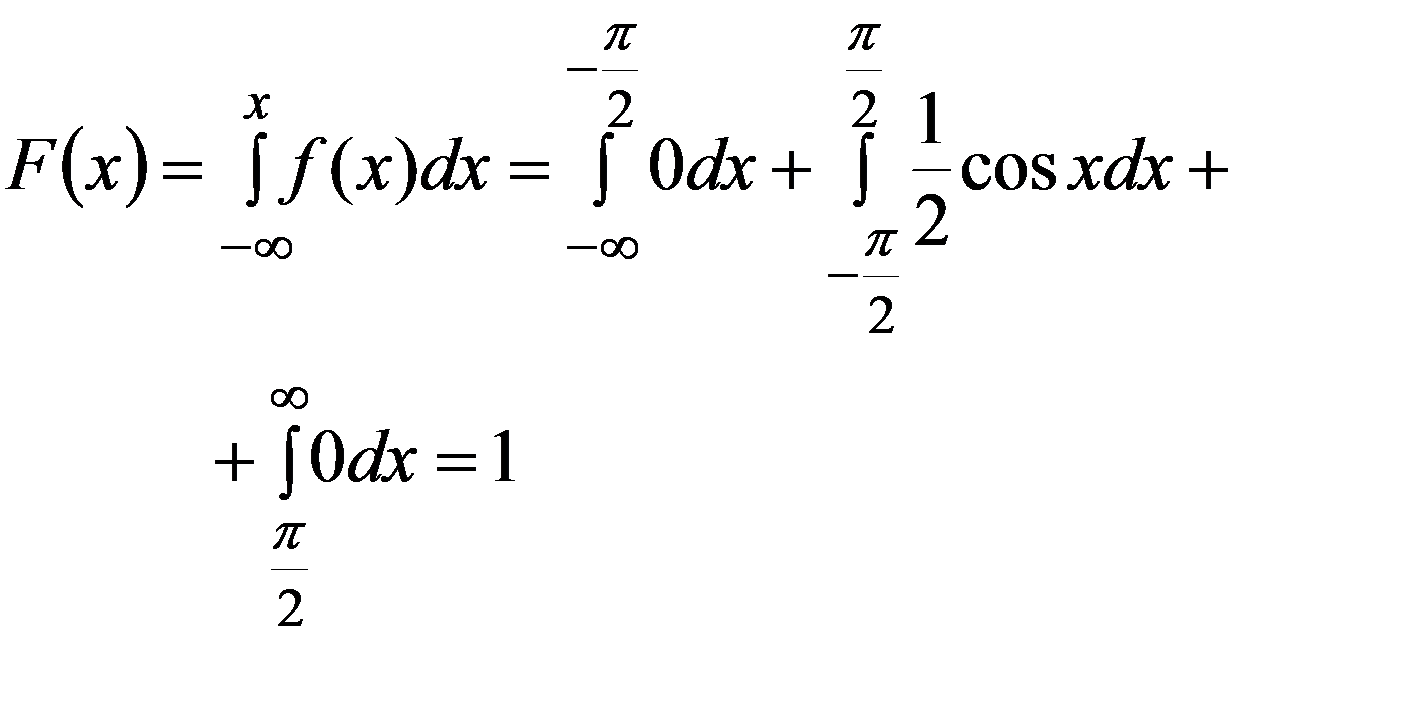

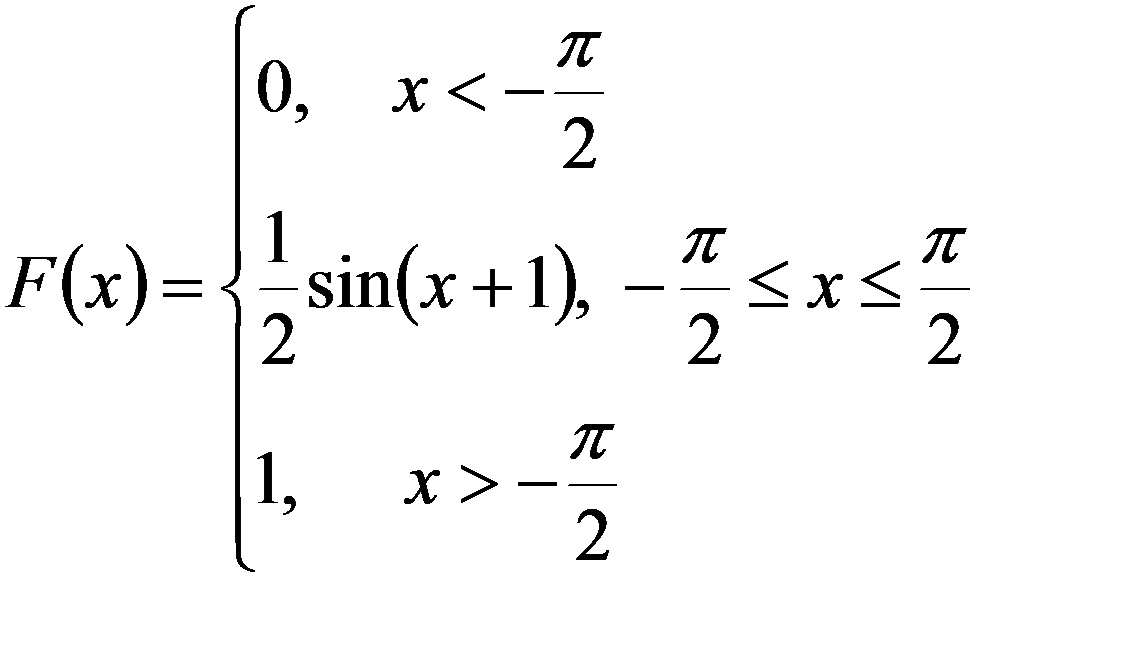
График функции F(x)

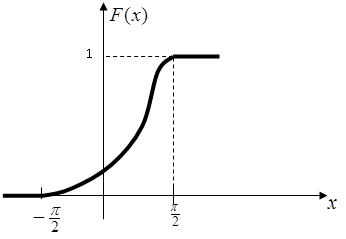
4.Согласно второму свойству F(x)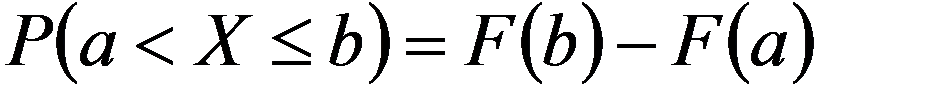

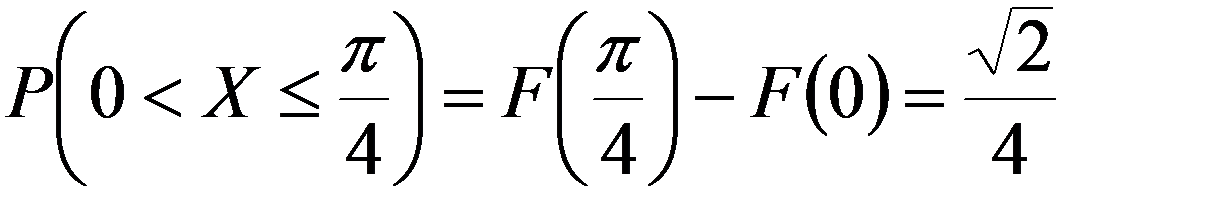
Числовые характеристики НСВ.

Математическое ожидание НСВ X с плотностью f(x) - среднее значение НСВ X , вычисляемое по формуле

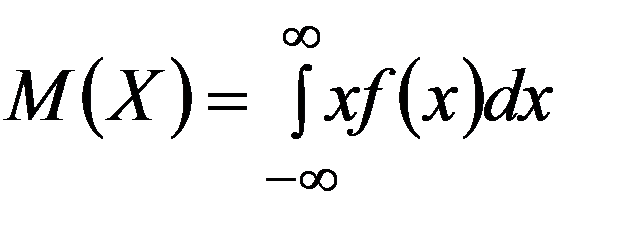(3.12)

или

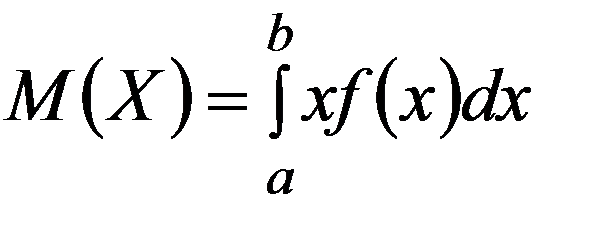(3.13)

eсли НСВ X принимает значение только из интервала (a,b) .

Мода НСВ X - значение x , в которой f(x) имеет максимум.

Медиана НСВ X геометрически – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

Дисперсия НСВ X

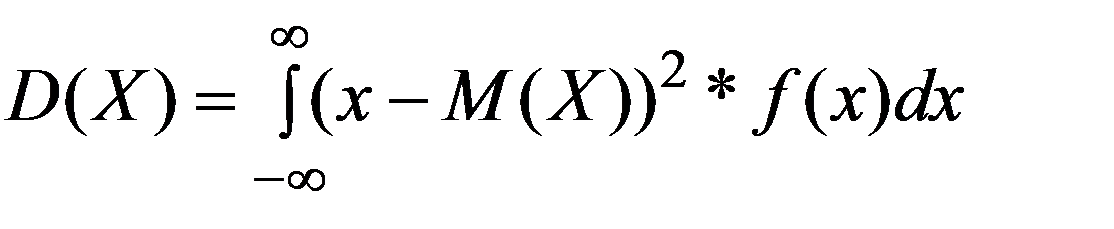(3.14)

или 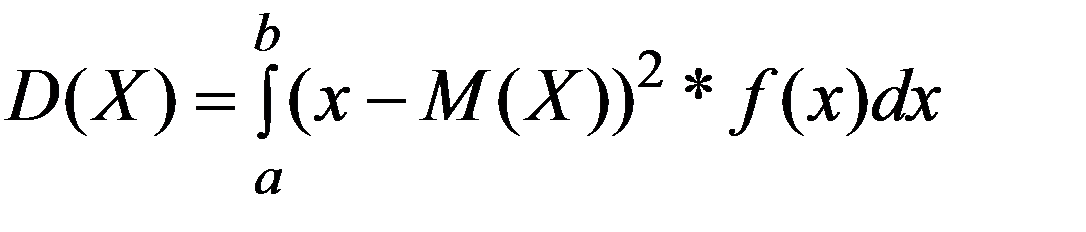(3.15)

СКО НСВ X

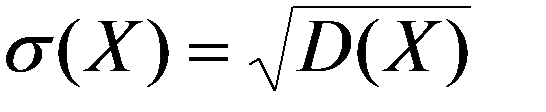(3.16)

Начальный теоретический момент k-го порядка НСВ X :

(3.17)

k = 0,1,2…

Центральный теоретический момент k -го порядка НСВ X :

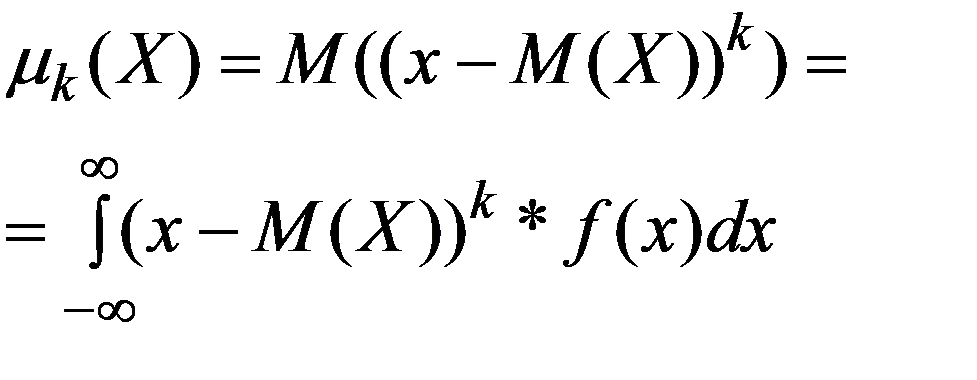(3.18)

k = 0,1,2…

Пример. Для НСВ X , функция распределения которой имеет вид: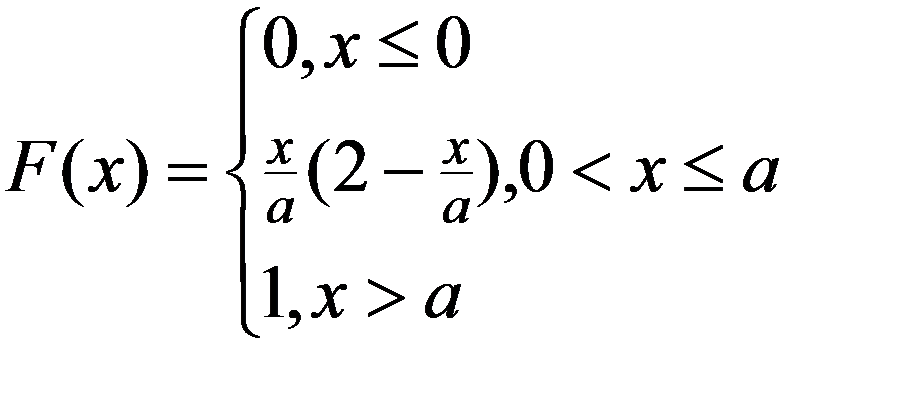

Найти числовые характеристики M(X), D(X), σ (X), µ₃ (X)

Решение:

1.По (3.7) определим f(x)

при x ≤ 0,

при 0 < x ≤ a ,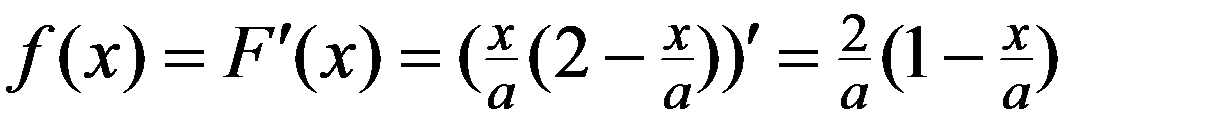

при x > a,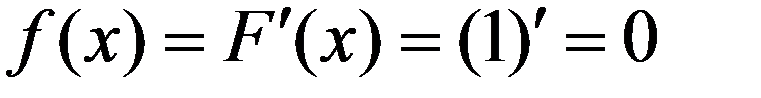

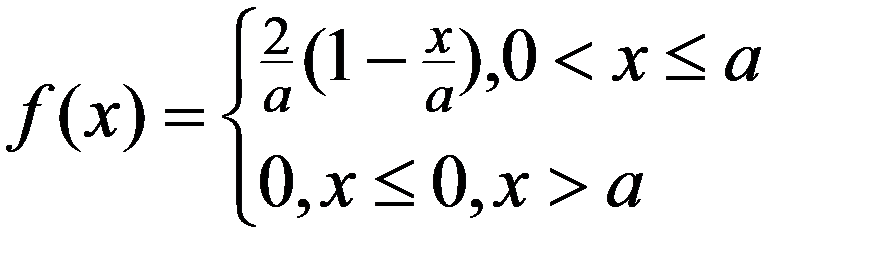
2. По (3.13)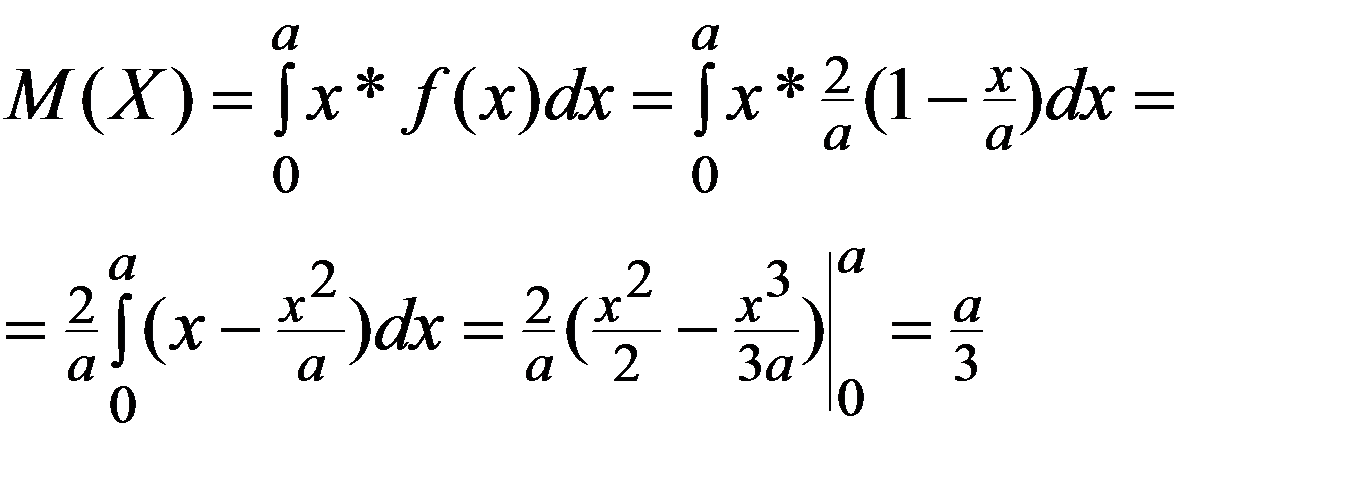

3. По (3.15)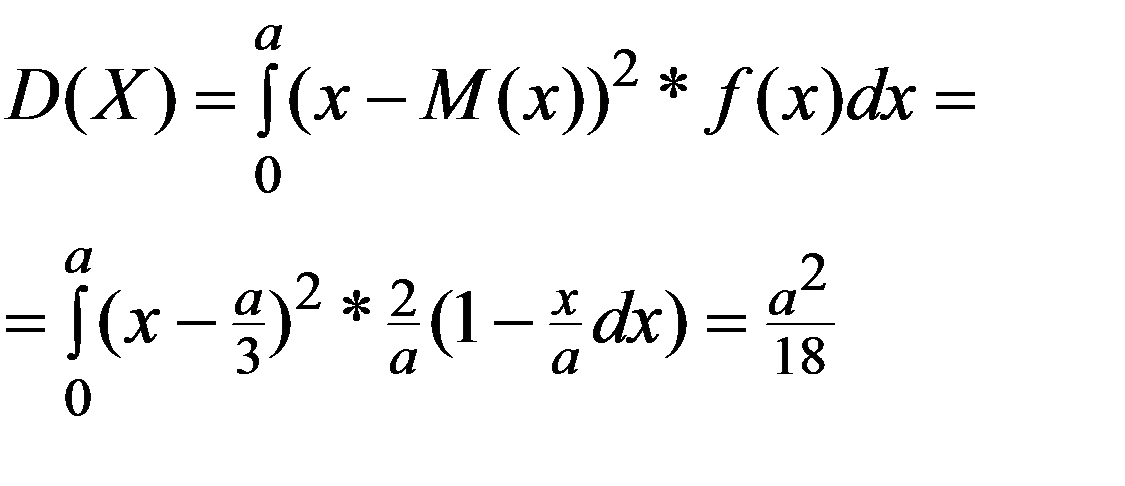

4. По (3.16)

5.

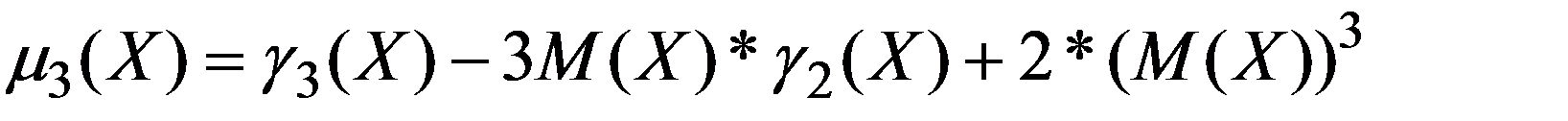
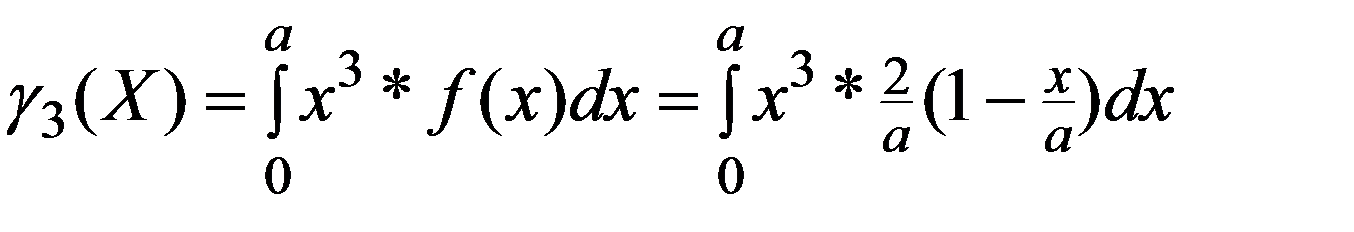
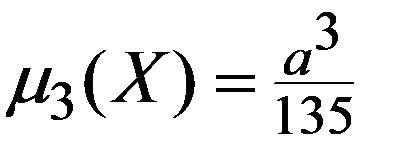
Основные (типовые) законы распределения НСВ.

НСВ X имеет равномерное распределение на участке (a,b) , если ее плотность на этом участке постоянна:

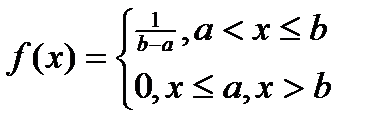
График f(x) имеет вид:

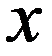
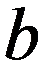
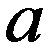
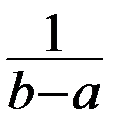
Функция распределения F(x)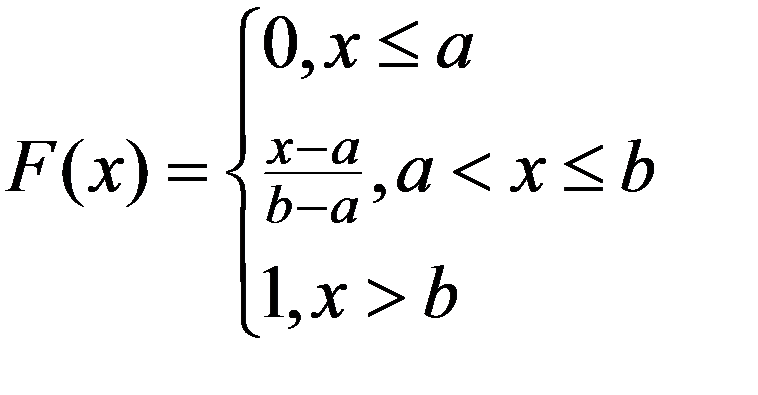

Равномерное распределение зависит от двух параметров a и b .

Числовые характеристики: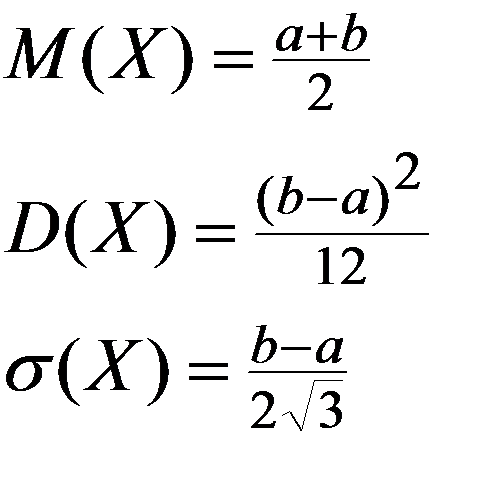

Частный случай равномерного закона распределения НСВ – НСВ R равномерно распределенная на интервале (0,1), для которой

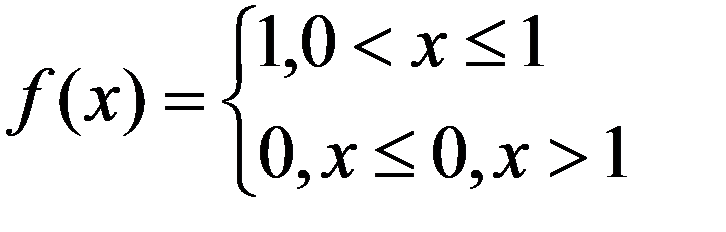
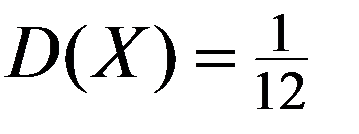
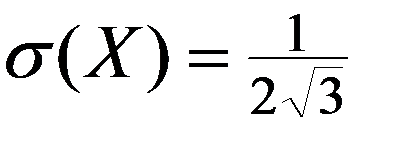
Значения НСВ 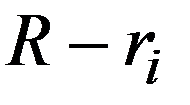называются случайными числами.

Вероятность попадания НСВ R в результате испытания в интервал (c,d) равна его длине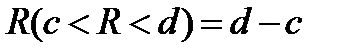

НСВ имеет показательное (экспотенциальное) распределение, если её плотность выражается формулой:

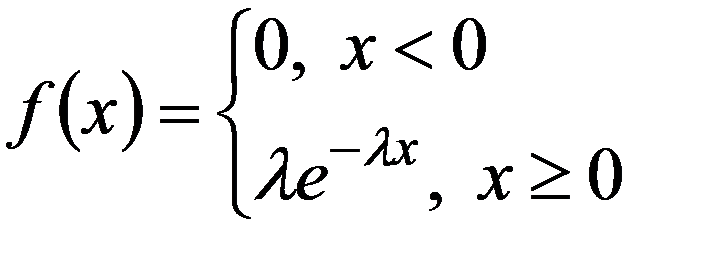
где λ - постоянная положительная величина.

График f(x) имеет вид

Функция распределения F(x)

График функции F(x)

Показательное распределение зависит от одного параметра λ .

Числовые характеристики:

, , ,

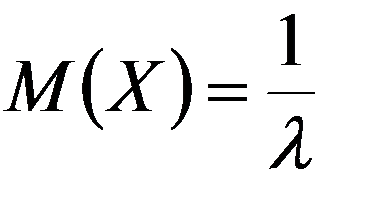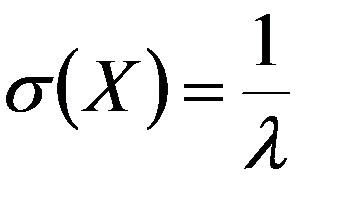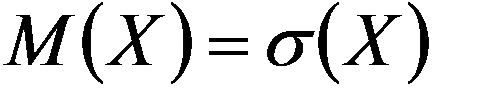
Вероятность попадания НСВ X , распределенной по показательному закону, в интервал (a,b) вычисляется по формуле:

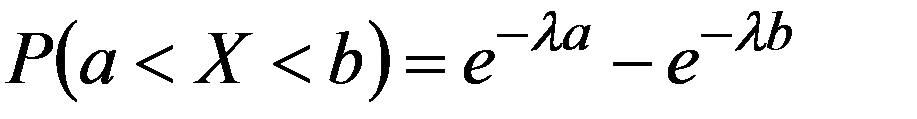(3.19)

Пример.

1. По соединительной линии между пунктами A и B осуществляются телефонные разговоры со средней длительностью 4 мин. для направления 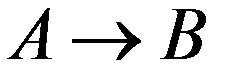и 3 мин. для 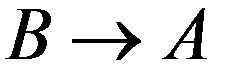. Вызовы 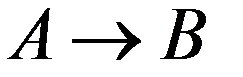составляют 55% всех вызовов. Найти вероятность того, что некоторый разговор длятся дольше 6 минут.

Решение.

Длительность разговора в телефонных сетях (время занятости линии связи) имеет показательное распределение. Если h - средняя длительность разговора, то λ = 1/h - интенсивность освобождения линии связи. И вероятность того, что разговор случайной длительностью τ закончится до момента t :

(3.20),

а вероятность того, что разговор не закончится до момента t :

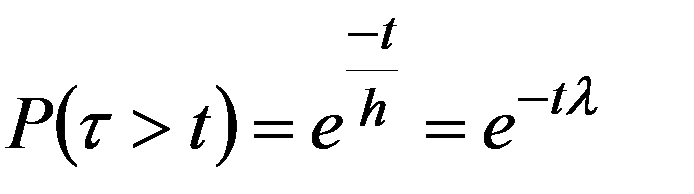(3.21)

Тогда

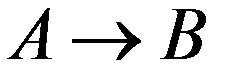
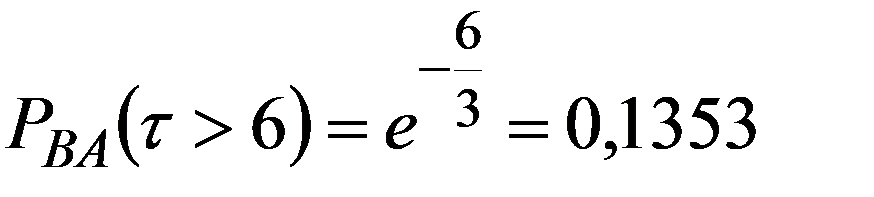
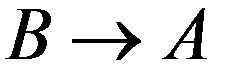
По формуле полной вероятности (2.20)

Пример 2.Элемент отказывает в среднем 1 раз за 50 часов непрерывной работы. Считая, что время безотказной работы распределено по показательному закону, найти вероятность отказа за 100 часов.

Решение.

Пусть элемент начинает работать в момент t₀ = 0 , а через время t происходит отказ. Обозначим через T НСВ - время безотказной работы элемента.

Тогда интегральная функция

(3.22)

определяет вероятность отказа за время t , а функция надежности

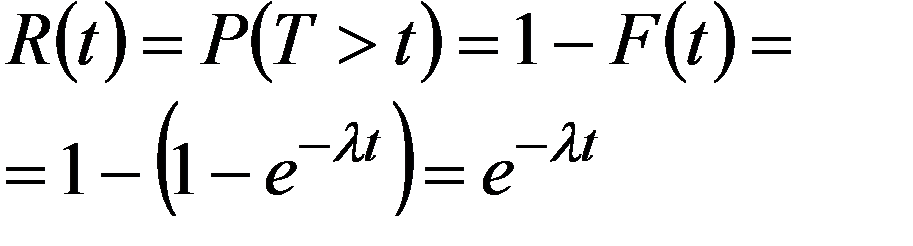(3.23)

где λ - интенсивность отказов, определяет время безотказной работы за время t .

Из анализа формулы R(t) следует, что вероятность безотказной работы элемента на интервале t не зависит от времени работы до начала рассматриваемого интервала, а зависит только от длительности времени t .

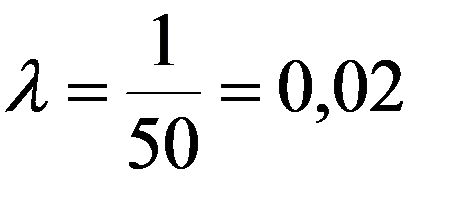
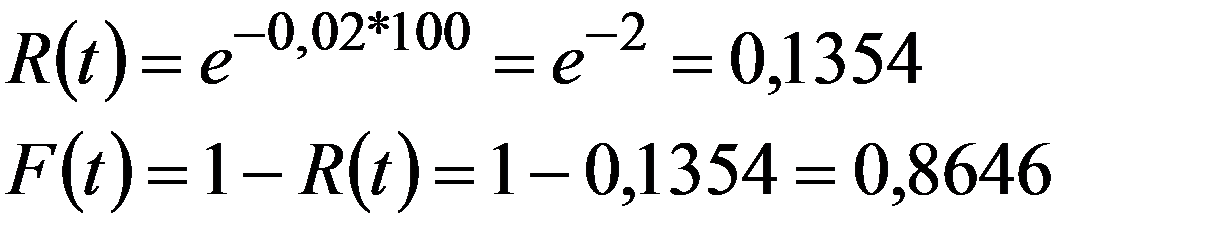
НСВ X имеет общее нормальное распределение с произвольными значениями m_x и σ_x , если её плотность

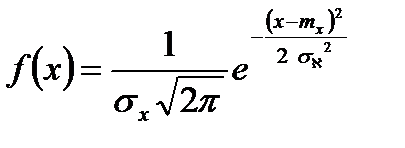(3.24)

или нормированное распределение с параметрами m_x = 0 и σ_x = 1, если её плотность

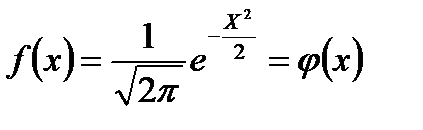(3.25)

есть функция Гаусса φ(x) .

График плотности нормального распределения называют нормальной кривой (кривой Гаусса)

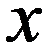
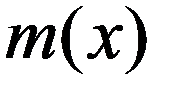
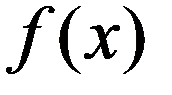
Нормальная кривая.

1. Определена на всей оси x

2. Принимает только положительные значения.

3. Ось 0x является горизонтальной асимптотой графика f(x).

4. Имеет только один максимум в точке m_x.

5. Симметрична относительно прямой X = m_x .

6. Точки на кривой с координатами 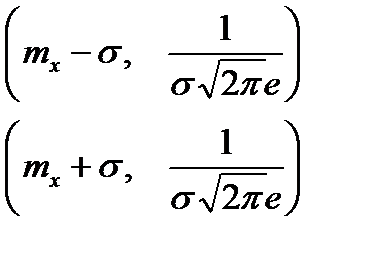являются точками перегиба.

При изменении m_x форма нормальной кривой не изменяется, она сдвигается вдоль оси 0x вправо, если m_x возрастает, и влево, если m_x уменьшается.

Изменение σ_x изменяет форму нормальной кривой. При возрастании σ_x кривая становится более пологой, т.е. прижимается к оси 0x . При уменьшении σ_x кривая становится более острой.

Интегральная функция F(x) общего нормального распределения

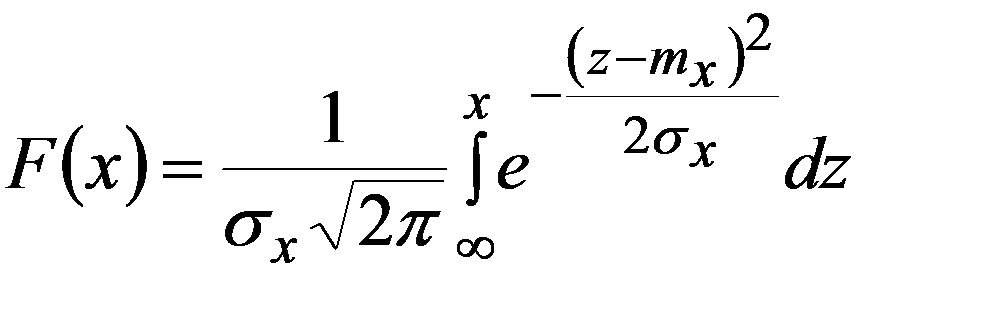(3.26)

а нормированного распределения

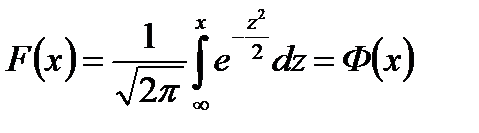(3.27)

есть функция Лапласа Ф(х)

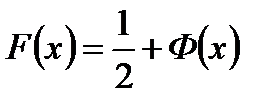(3.28)

Нормальное распределение зависит от двух параметров m_x и σ_x.

Вероятность попадания НСВ X в интервал (a,b)

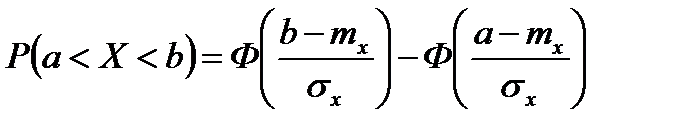(3.29)

Если участок (a,b) симметричен относительно точки m_x , то вероятность попадания в него

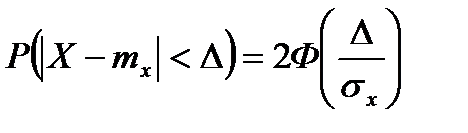, где 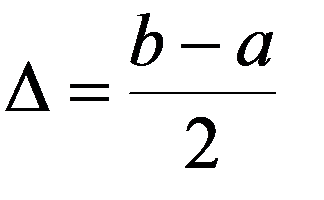- половина длины участка.

Пример.

1.Проверить правило 3-х сигм

Решение.

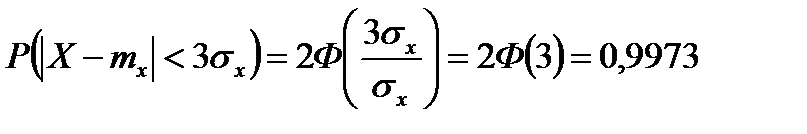
т.е. возможные значения нормальной НСВ X попадут в интервал 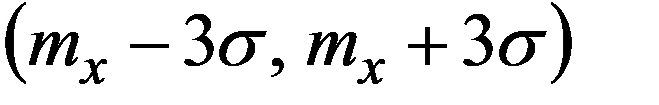с вероятностью P=0,9973.

Пример 2. На автоматическом токарном станке изготовляют болты, номинальная длина которых 40мм. В процессе работы станка наблюдаются случайные отклонения, распределенные по нормальному закону с m_x = 0 и σ_x . При контроле бракуются все болты, размеры которых отличаются от номинального больше, чем на 2мм. Найти σ_x отклонение, если известно, что брак составляет 10% всей продукции.

Решение.

X - отклонение размера случайно взятого болта от номинального

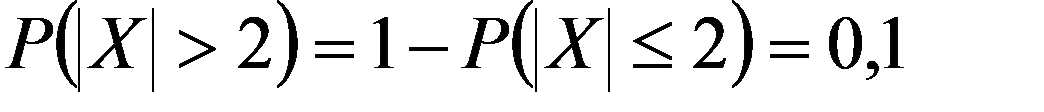
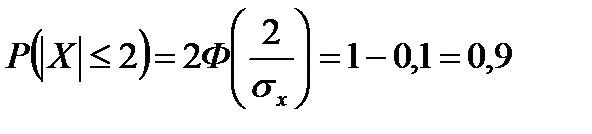
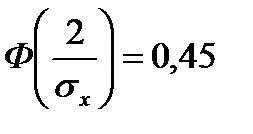
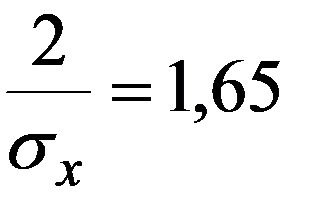
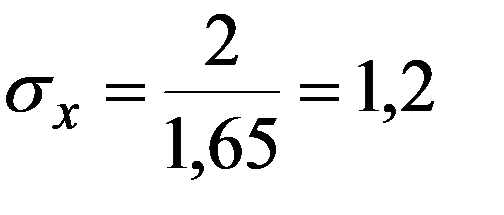
Нормальный закон является наиболее важным, как в теории, так и на практике, т.к. большинство наблюдаемых явлений подчиняются этому закону и он считается предельным законом, к которому приближаются другие законы распределения при определенных часто встречающихся типичных условиях.

Система двух СВ (двумерная СВ)

Система двух СВ – это совокупность двух СВ X и Y , рассматриваемых совместно (как единое целое). Каждую из величин X , Y называют составляющей (компонентой) двумерной СВ. Обозначают двумерную СВ (X,Y), а возможные значения (x,y) . Геометрически система двух СВ (X,Y) интерпретируется как случайная точка с координатами (X,Y) на плоскости x0y .

Различают

-дискретные двумерные СВ (составляющие X,Y - дискретны)

-непрерывные двумерные СВ (составляющие X,Y - непрерывны)

Система двух СВ может быть полностью представлена законом распределения, частично – числовыми характеристиками.

Законом распределения вероятностей двумерной СВ называют соответствие между возможными значениями СВ и их вероятностями.

Закон распределения двумерной СВ может быть задан

1) таблично;

2) интегральной функцией распределения;

3) дифференциальной функцией распределения (двумерной плотностью распределения).

Для дискретных двумерных СВ закон распределения имеет вид 1 или 2, для непрерывных – 2 или 3. Функция распределения – универсальный способ представления закона распределения системы двух СВ.