Формы закона распределения дискретной случайной величины.
Ряд распределения дискретной случайной величины - это таблица, в которой перечислены в порядке возрастания все возможные различные значения этой случайной величины 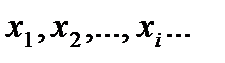 с соответствующими им вероятностями
с соответствующими им вероятностями 

| 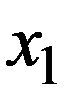
| 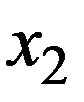
| 
| 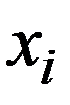
| 
|
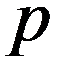
| 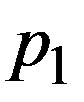
| 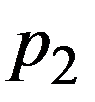
| 
| 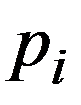
| 
|
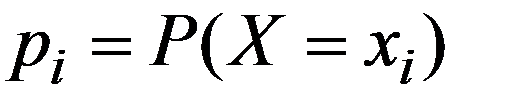
Т.к. в результате испытания X принимает только одно из приведенных значений, то события X=x1, X=x2 ,…, X=xi , … образуют полную группу и 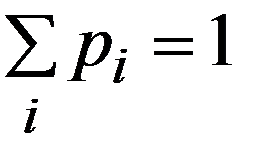 (3.1)
(3.1)
Формула (3.1) называется условием нормировки ДСВ.
Многоугольник распределения ДСВ – графическое изображение ряда распределения ДСВ в декартовой системе координат.
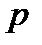
|
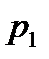
|
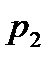
|
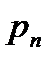
|

|
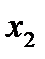
|
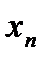
|
|
Многоугольник распределения для ДСВ X, принимающей значения x1, x2, … , xn с вероятностями p1, p2, … , pn соответственно.
Аналитическая форма представление закона распределения ДСВ с помощью формулы
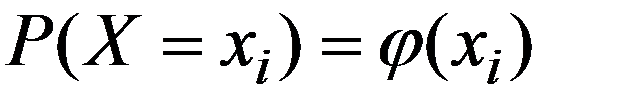
Функция распределения F(x) ДСВ X есть разрывная, ступенчатая функция, скачки которой соответствуют возможным значениям x1, x2, … случайной величины X и равны вероятностям p1, p2, … этих значений. Между скачками функция F(x) сохраняет постоянное значение. В точке разрыва функция F(x) равна тому значению, с которым она подходит к точке разрыва слева, т.е. F(x) - непрерывна слева.
|
|
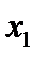
|
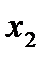
|
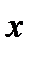
|

|
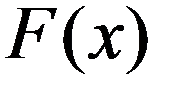
|
График функции распределения ДСВ X , принимающей значения x1, x2, … , xn .
Плотность распределения не используется для представления закона распределения ДСВ.
Пример. Устройство состоит из 3-х независимо работающих элементов. Вероятность того, что элемент не сработает в данном испытании 0,1. Привести все формы представления закона распределения случайной величины X равной числу несработавших элементов.
Решение.
X - ДСВ. Возможные значения
x1 = 0 - все элементы работающие;
x2 = 1 не сработал 1 элемент;
x3 = 2 не сработало 2 элемента;
x4 = 3 не сработали 3 элемента.
Вероятность каждого из возможных значений ДСВ X можно рассчитать по формуле Бернулли (2.22), которая для данного примера будет являться аналитической формой закона распределения.
n=3 , p=0,1, q=1-0,1=0,9
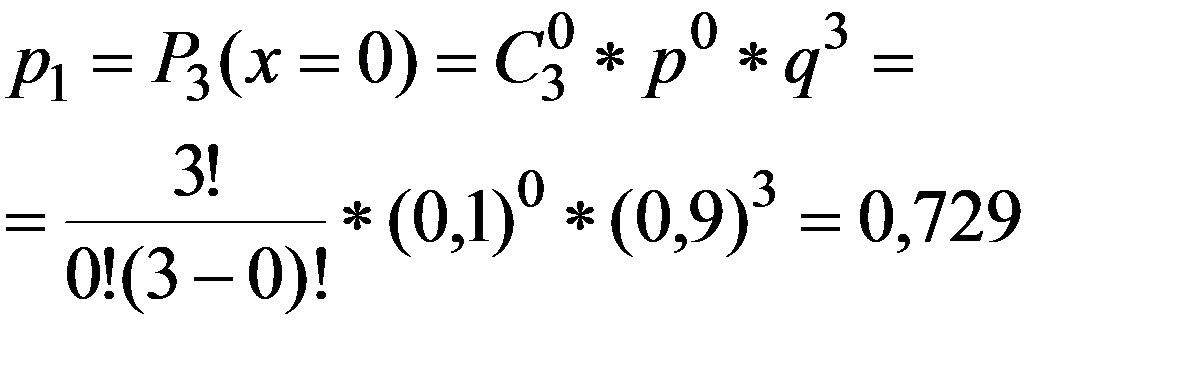
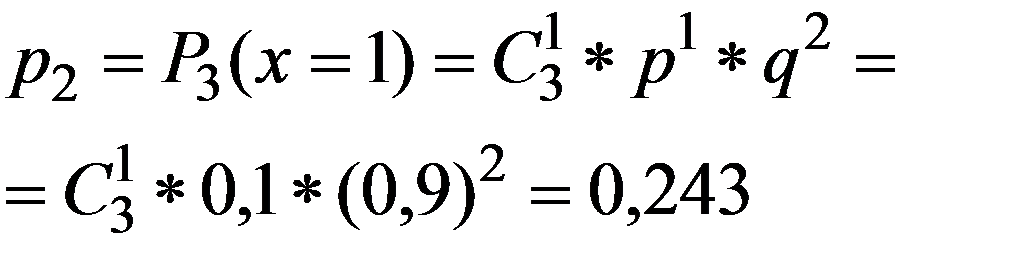
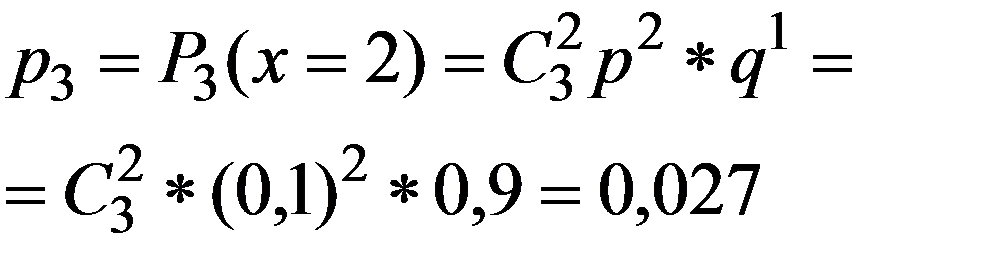
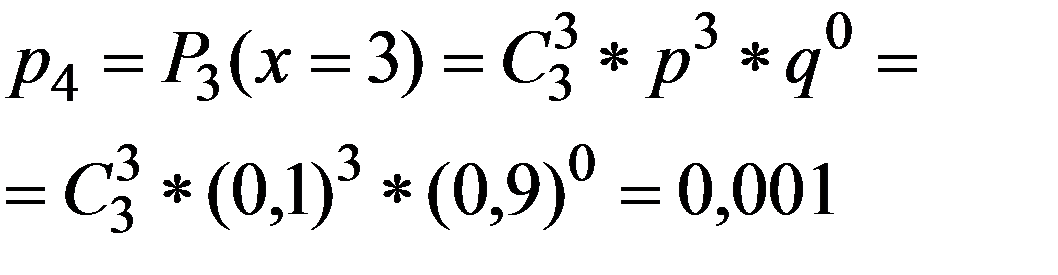
Проверим (3.1)
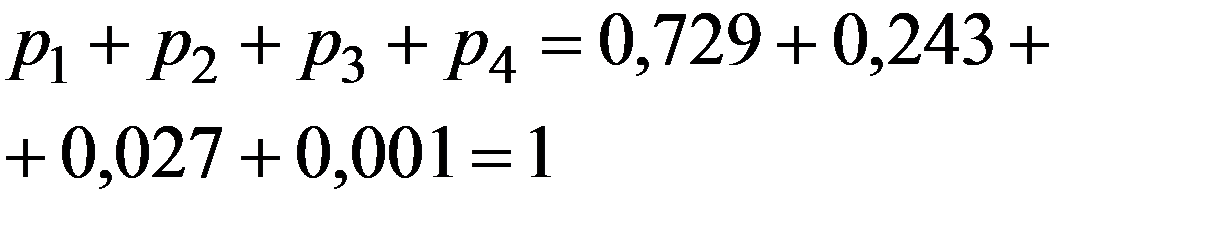
Запишем ряд распределения ДСВ
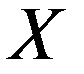
| ||||
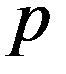
| 0,729 | 0,243 | 0,027 | 0,001 |
Построим многоугольник распределения (схематично):

|
| 0,729 |
| 0,243 |
| 0,027 0,001 |
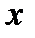
|
Построим функцию распределения.
Если x ≤ 0, то X < x - невозможное событие и F(x) = 0
Если 0 < x ≤ 1 , то F(x) = p1 = 0,729 т.к. событие X < x равнозначна событию X = 0
Если 1 < x ≤ 2 , то 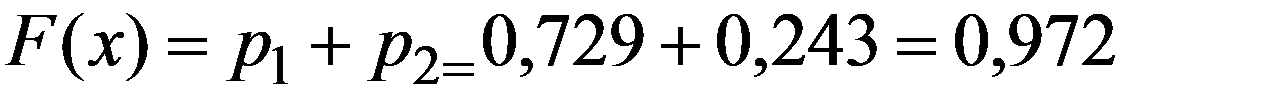
Cобытие X < x может быть осуществлено, когда X примет значение x1 или x2 .
Поскольку события X = x1, X = x2 - несовместны и независимы, то F(x) = P(X < x) равна сумме вероятностей P(X=x1) и P(X=x2) .
Если 2 < x ≤ 3 то 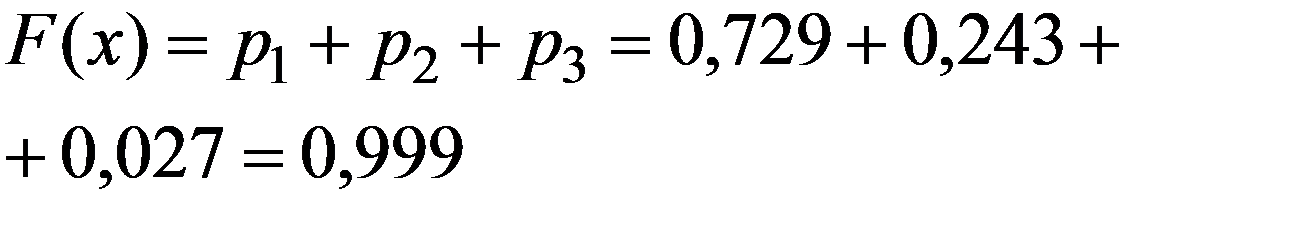
Если x > 3, то F(x) = 1 , т.к. событие X < x является достоверным.
Итак
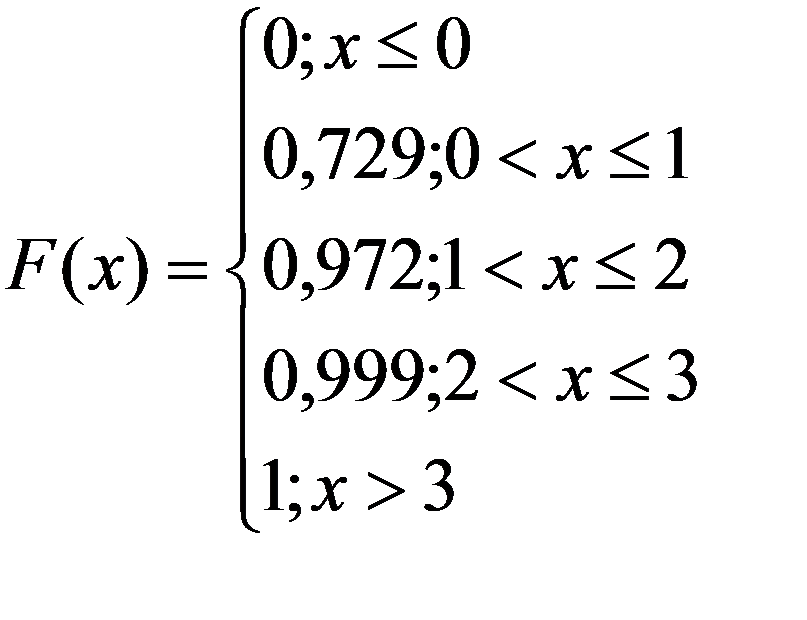
Построим график функции распределения:
| 0,729 |
| 0,999 0,972 |
|
|
Дата добавления: 2015-12-26; просмотров: 1298;
