Основные (типовые) распределения ДСВ
СВ X называется распределенной по биномиальному закону, если её возможные значения 0,1,2,…,n, а соответствующие вероятности рассчитываются по формуле Бернулли (2.22)
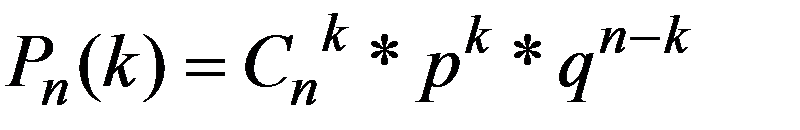
k = 0,1,2,…,n
k - число появления события в независимых испытаниях.
Биномиальное распределение зависит от двух параметров p и n .
Ряд распределения имеет вид:
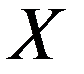
| … | 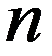
| |||
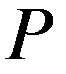
| 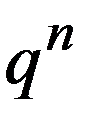
| 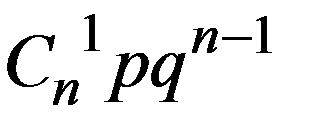
| 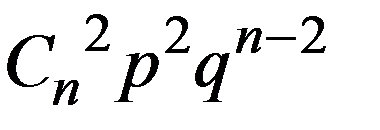
| 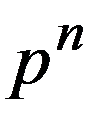
|
M (X) = n*p D(X) = n*p*q (3.6)
Пример. Проверить формулы (3.6) для примера рассмотренного выше.
Решение.
n=3 , p=0,1 , q=0,9
M(X) = 3*0,1 = 0,3
D(X) = 3*0,1*0,9 = 0,27
ДСВ называется распределенной по закону Пуассона, если её возможные значения 0,1,2,…,n, а соответствующие вероятности выражаются формулой Пуассона (2.24)
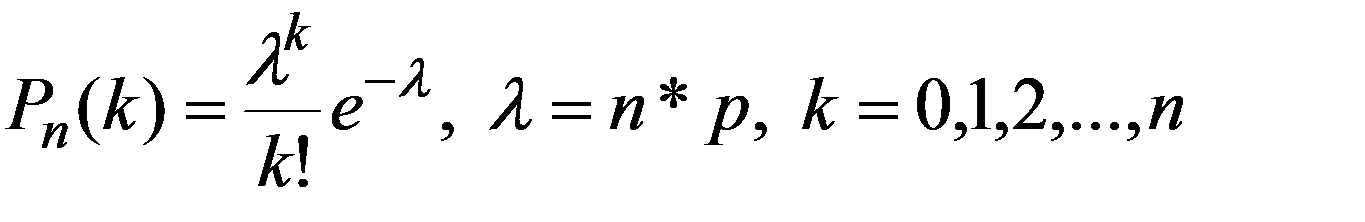
Распределение Пуассона зависит от одного параметра λ - среднее число появления событий при испытаниях.
Ряд распределения имеет вид:
| X | … | 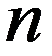
| |||
| P | 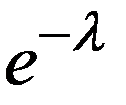
| 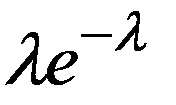
| 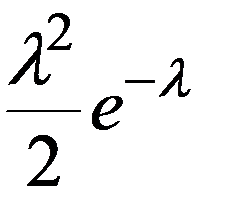
| 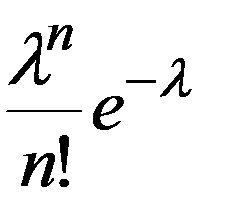
|
M(X) = D(X) = λ = n*p
Пуассоновское распределение является предельным для биномиального при 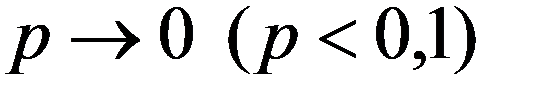 ,
, 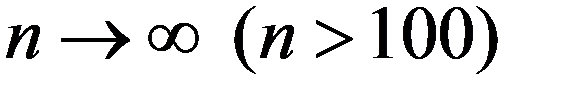 , если
, если 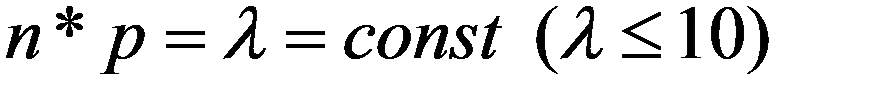 .
.
Пример1.
Устройство имеет 1000 элементов, которые работают независимо один от другого. Вероятность того, что элемент выйдет из строя во время работы p=0,004. Определить среднее количество элементов, которые могут выйти из строя.
Решение.M(X) = n*p = 1000*0,004 = 4
Пример2.
На АТС на протяжении часа поступает в среднем 30 вызовов. Найти вероятность того, что на протяжении минуты поступит не более 2-х вызовов.
Решение.
M(X) = 30/60 = ½ = 0,5 - среднее числo вызовов за одну минуту
λ = M(X) = 0,5
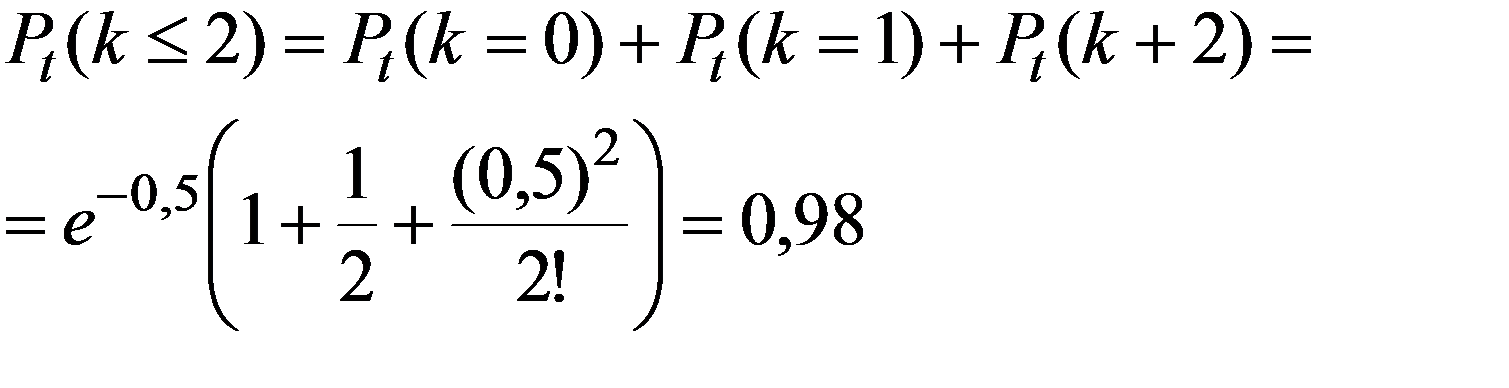
ДСВ X называется распределенной по гипергеометрическому закону, если её возможные значения 0,1,2,…, min (M,n) , а соответствующие вероятности определяются гипергеометрической формулой
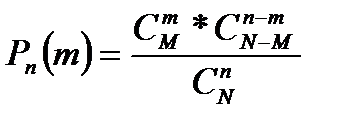 (1.7).
(1.7).
m = 0,1,2,…,min (M,n)
Гипергеометрическое распределение зависит от трех параметров n, N, M.
Ряд распределения имеет вид:
| X | … | 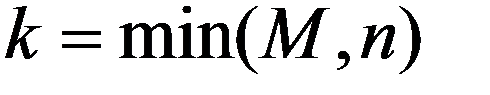
| |||
| P | 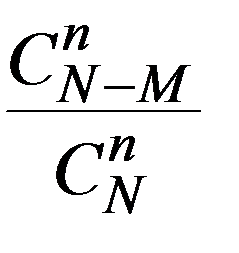
| 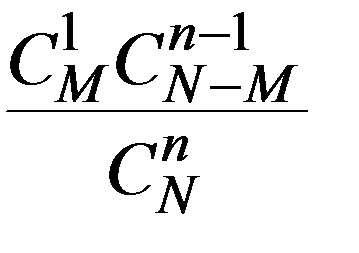
| 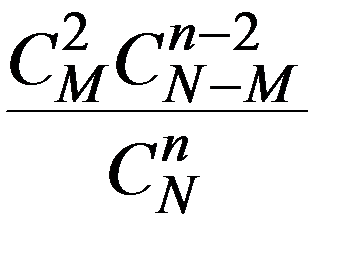
| 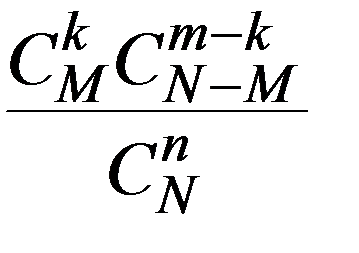
|
M(X) = 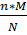
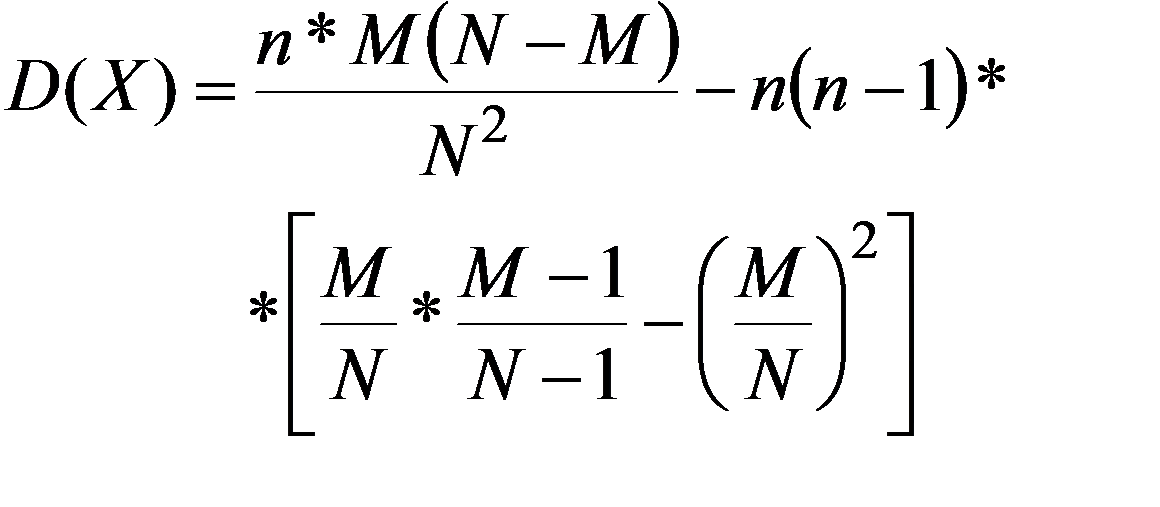
При n < 0,1*N гипергеометрическое распределение дает вероятности, близкие к вероятностям, найденным по биномиальному закону.
Пример. В ящике имеется 10 однотипных деталей, из них 7 стандартных. Из ящика берут 4 детали. Построить ряд распределения ДСВ – числа стандартных деталей среди отобранных.
Решение.
| X | ||||
| P | 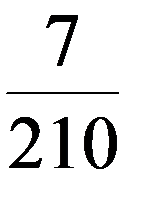
| 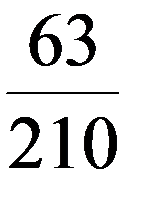
| 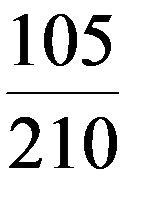
| 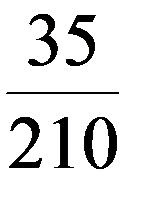
|
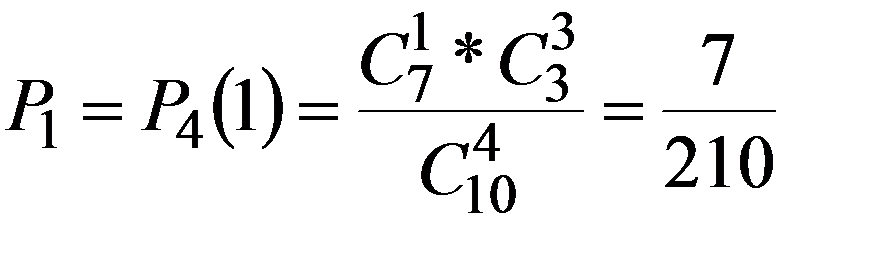
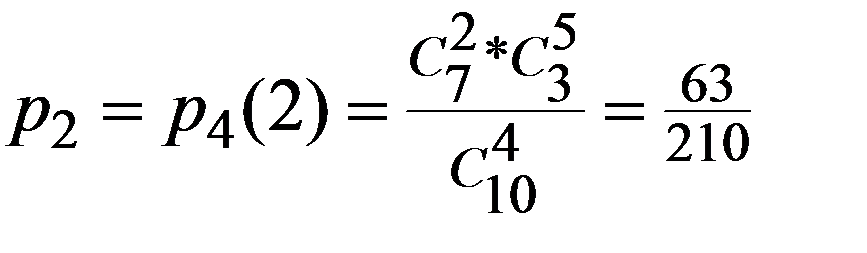
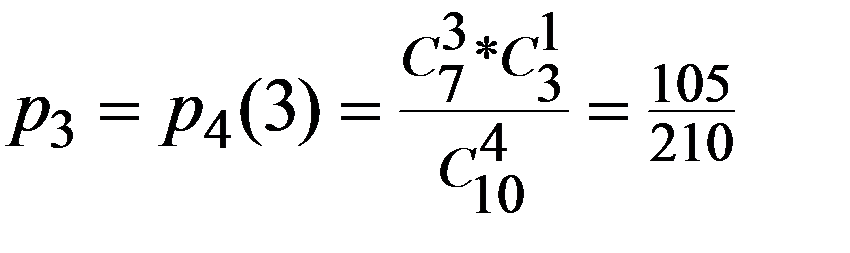
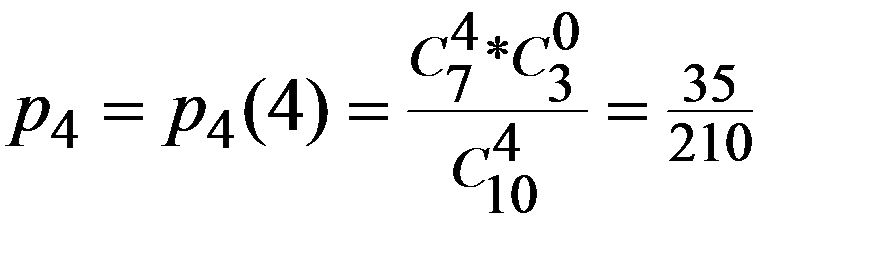
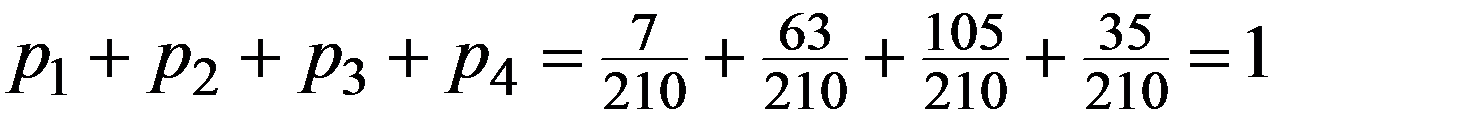
ДСВ называется распределенной по равномерному закону, если ее возможные значения 0,1,2,…,n-1 , а соответствующие им вероятности можно рассчитать по формуле
Pn(k) = 1/n, k = 0,1,2,…,n-1
Равномерное распределение зависит от одного параметра n/
Ряд распределения имеет вид:
| X | … | n - 1 | ||
| P | 1/n | 1/n | … | 1/n |
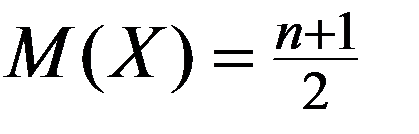
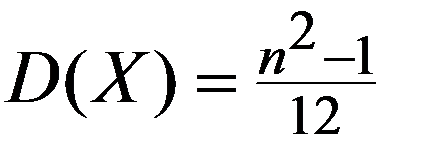
Пример. На связке 5 ключей, из которых только один подходит к замку. Составить ряд распределения ДСВ числа ключей, которые пробуются для открытия замка.
| X | |||||
| P | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
p1 = 1/5
p2 = 4/5 * ¼ = 1/5
p3 = 4/5 * ¾ * 1/3 = 1/5
p4 = 4/5 * ¾ * 2/3 * 1/2 = 1/5
p5 = 4/5 * ¾ * 2/3 * ½ * 1 = 1/5
ДСВ X имеет геометрическое распределение, если ее возможные значения 0,1,2,… а вероятности этих значений 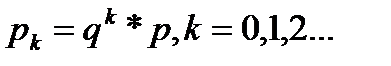 .
.
Вероятности pk для ряда последовательных значений k образуют бесконечно убывающую геометрическую прогрессию со знаменателем q.
Ряд распределения имеет вид:
| X | … | k | … | |||
| p | p | q*p | q2 * p | … | qk * p | … |
M(X) = q/p D(X) = q / p2
Нередко рассматривают СВ Y=X+1 , равную числу попыток до получения результата, включая удавшуюся попытку, т.н. геометрическое распределение начинающееся с «1», для которого 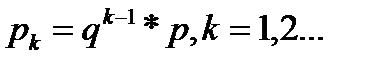
Ряд распределения СВ Y :
| Y | … | k | … | ||
| p | p | q * p | … | 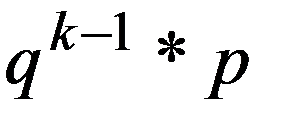
| … |
M(Y) = 1/p, D(Y) = q / p2
Геометрическое распределение зависит от одного параметра p .
Пример. Из корзины, в которой 3 черных и два белых шара последовательно вынимают шары до появления белого. Перед очередным извлечением шара, вынутый ранее шар возвращается в корзину. Построить ряд распределения ДСВ X - числа вынутых белых шаров до появления черного и ДСВ Y - количество попыток до появления черного шара.
Решение:
| X | … | |||
| p | 3/5 | 2/5 * 3/5 | 2/5 * 2/5 * 3/5 | … |
| Y | … | |||
| p | 3/5 | 2/5 * 3/5 | 2/5 * 2/5 * 3/5 | … |
Непрерывные СВ
Непрерывной СВ в широком смысле называется СВ, которая может принимать все (бесконечно много) значения из некоторого конечного или бесконечного промежутка. Если функция распределения F(x) везде непрерывна и имеет производную, СВ X называется непрерывной в узком смысле.
Пример.
1.Координаты точки попадания при выстреле.
2.Время опоздания поезда.
3.Время безотказной работы лампы.
Дата добавления: 2015-12-26; просмотров: 1250;
