Деление отрезка в заданном отношении

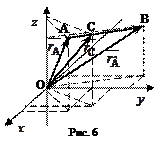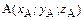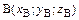Пустьв прямоугольной системе координат задан произвольный отрезок АВ, где граничные точки отрезка имеют координаты , , а также известно, что внутренняя точка С этого отрезка делит отрезок АВ в отношении 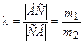(рис. 6). Тогда радиус-вектор точки С определяется по формуле

.

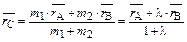В координатной форме данную зависимость можно переписать так:

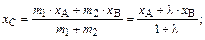
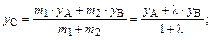
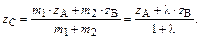
В частном случае, когда точка С является серединой отрезка АВ, формулы преобразуются к виду:

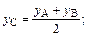
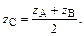
Пример.Найти координаты точки С, делящей отрезок АВ в отношении 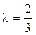, если А(2; 4; –1), B(–3; –1; 6).

Решение.Воспользуемся расчетными формулами:

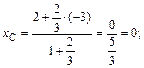
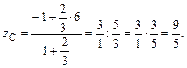
Таким образом, точка С имеет координаты С(0; 2; ).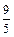

Литература:[1, гл. 1, §1.3].

1.6. Линейная зависимость векторов**

Векторы 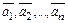линейно независимы, если из равенства

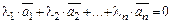
следует, что .В противном случае векторы называются линейно зависимыми.

Если произвольный вектор можно представить в виде 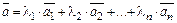, то говорят, что этот вектор линейно выражается через векторы .

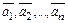Справедливы следующие утверждения:

1) векторы (при 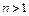)линейно зависимы тогда и только тогда, когда, по крайней мере, один из них линейно выражается через остальные;

2) если векторы 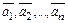линейно независимы, то ни один из них нельзя выразить через остальные; в частности, ни один из них не может быть нулевым;

3) векторы линейно зависимы тогда и только тогда, когда один из векторов является линейной комбинацией остальных.

Пример.Разложить вектор 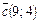по векторам 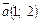и .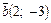

Решение. ; ; ; .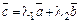

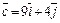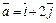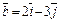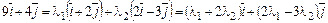. Нахождение неизвестных параметров l₁ и l₂ сведем к решению системы:

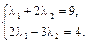
Систему решим методом Крамера:

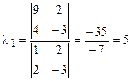; . Тогдавектор 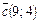в разложении по векторам 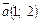и 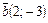будет иметь следующий вид: .

Литература: [ 1, гл. 5, § 5.11];[3, гл.2, п. 12.5].