Смешанное произведение тройки векторов,

его свойства и применение*

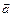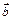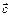Смешанным произведением векторов , и называется число, равное скалярному произведению вектора 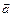на вектор, равный векторному произведению векторов 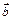и 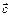.Обозначается как .

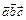Смешанное произведение векторов обладает следующими свой­ствами:

1. Смешанное произведение равно нулю, если:

а) хотя бы один из векторов нулевой;

б) в произведении есть коллинеарные векторы;

в) векторы компланарны.

2. .

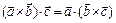3. .

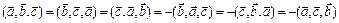4. .

В координатной форме смешанное произведение векторов 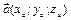, и 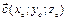равно:

.

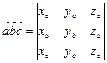Применение смешанного произведения векторов.

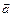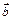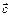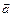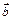1.Проверка тройки векторов на компланарность. Векторы , и компланарны тогда и только тогда, когда их смешанное произведение равно нулю при условии, что ¹ , 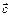¹ , ¹ :

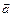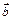векторы , и 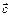компланарны.

Пример 1. Доказать, что точки А(5; 7; 2), B(3; 1; –1), C(9; 4; –4), D(1; 5; 0) лежат в одной плоскости.

Решение.Если заданные точки лежат в одной плоскости, то соответствующая тройка векторов, выходящих из общего начала, будет компланарна. Проверим, компланарны ли векторы с общим началом в точке А. Найдем координаты этих векторов: 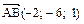, , 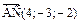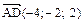. Вычислим их смешанное произведение:

.

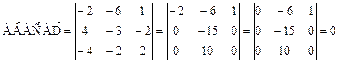Таким образом, полученные выше векторы компланарны, следовательно, точки A, B, C и D лежат в одной плоскости.

2.Определение взаимной ориентации тройки векторов в пространстве. Тройка векторов 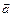, 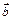и 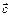в пространстве право­ориентирована, если ,и левоориентирована при .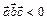

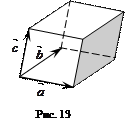3.Нахождение объемов. Смешанное произведение 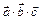по модулю равно объему параллелепипеда, построенного на векторах 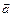, 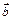и 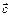, как на сторонах (рис. 13), т.е.

.

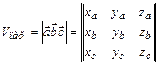Объем треугольной пирамиды, построенной на векторах 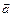, 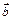и 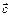, как на сторонах (рис. 14), равен одной шестой смешанного произведенияэтих векторов, взятого по абсолютной величине, т.е.

.

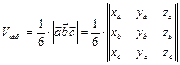Пример 2. Найти длину высоты треугольной пирамиды с вершинамиA(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2), опущенную на грань BCD.

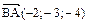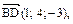
Решение.Даны координаты векторов: , 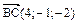. Тогда объем пирамиды можно вычислить по формуле

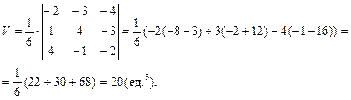
Из школьного курса математики известно, что 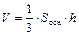. Откудаследует, что 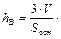Поэтому для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.

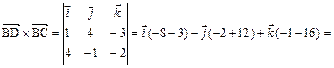
Определим модуль векторного произведения векторов:

.

Тогда площадь треугольника BCDравнаS_осн = 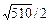(ед.²), а длина искомой высоты – (ед.).

Литература: [3, гл. 2, п. 12.13]; [4, гл. 2, §8].