Операции над векторами в координатах

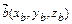Пусть заданы векторы и в прямоугольной системе координат.Линейные операции над ними выполняютсяпо следующим формулам:

.

Пример1. Даны два вектора и 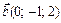. Найти координаты и длину вектора .

Решение. ; ; ; .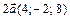

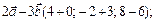
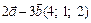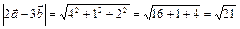Пример2.Дан вектор 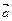, образующий с осью 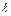угол 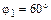, и вектор 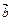, образующий с той же осью угол 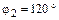. Найти проекцию суммы 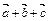, где 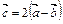, на ось 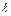, если известно, что , .

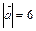Решение.Так как проекция суммы векторов равна сумме их про­екций, необходимо найти проекцию каждого слагаемого на ось .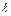

;

;

.

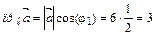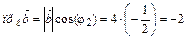Тогда 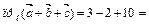11.

Понятие радиус-вектора точки. Координаты и длина вектора, заданного граничными точками.

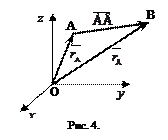Рассмотрим в прямоугольной декартовой системе координат произвольную точку М. Координаты вектора 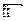будем называть координатами точки М. Вектор 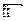называется радиус-вектором точки М и обозначается .

Найдем координаты вектора 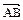, если известны координаты начальной и конечной точек (рис. 4).

Нетрудно заметить, что .Тогда согласно введенным для векторов операциям имеем

.

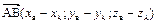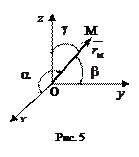Рассмотрим радиус-вектор 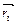точки 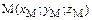в прямоугольной системе координат . Пусть 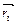образует с осями координат 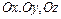соответственно углы 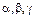(рис. 5).

Направление вектора 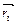определяется с помощью направляющих косинусов , , , 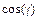которыеравны:

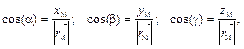
где .

Пример 3.Найти координаты вектора 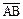и его длину, если , .

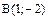Решение. Найдем координаты вектора :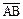

.

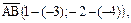
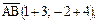
Тогда длина вектора будет равна

.

Пример 4. Найтинаправляющие косинусы вектора , если , .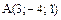

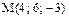Решение.Найдем координаты вектора :

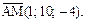
Тогда его длина и направляющие косинусы будут соответственноравны:

,

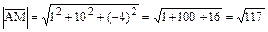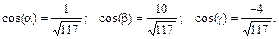
Условия коллинеарности и равенства векторов, заданных в координатах.

Пусть задан ненулевой вектор 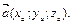Тогда любой коллинеарный с ним вектор будет отличаться от него на постоянный множитель, т.е. , где 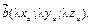Следовательно, у коллинеарных векторов 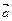и 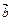координаты пропорциональны:

,

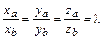причем, если: 1) l>0, то 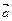и 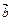сонаправлены;

2) l<0, то 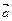и и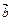меют противоположные направления;

3) 0<½l½<1, то 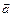корочевектора 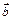в l раз;

4) ½l½>1, то 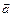длиннеевектора 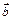в l раз.

Условием равенства двух векторов 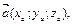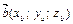является

.

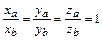Это означает, что координаты равных векторов совпадают.

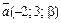Пример 5.Определить, при каких значениях параметров и векторы и 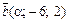коллинеарны. Как направлены эти векторы и как соотносятся их длины?

Решение.Из коллинеарностивекторов 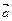и 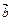будет следовать пропорциональность их соответствующих координат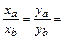 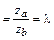. В нашем случае эти пропорции будут выглядеть следующим образом:

.

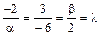Вторая пропорция полностью определена, откуда . Следовательно, , откуда a = 4. С другой стороны 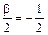, тогда b = –1.

Так как 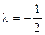, то векторы 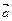и 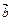имеют противоположные направления и вектор 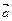в два раза короче вектора .

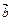Пример 6.Даны три вершины параллелограмма 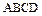: 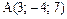; ; 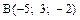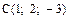. Найти его четвертую вершину .

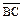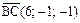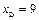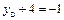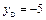Решение.Заметим, что вектор равен вектору , а значит координаты этих векторов равны. Найдем координаты этих векторов: , . Тогда или ; или ; или 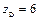. Таким образом, точкаDимеет координаты .

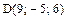Л и т е р а т у р а: [1,гл. 5, §§5.3, 5.5, 5.6];[2, гл.18,§§ 9–11];[3, гл.2, пп.12.6–12.8];[4, гл. 2, § 5, пп. 5.4, 5.5].