Координаты вектора и его длина

Элементы векторной алгебры

Векторы, основные понятия

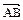Вектором называется направленный отрезок. Вектор с началом в точке А и концом в точке В обозначается символом (или , ,…).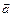

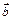Модулем (длиной) вектора 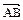называется расстояние от начальной точки А до конечной точки В вектора и обозначается , .

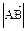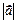Единичным(или ортом) называется вектор 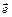, длина которого равна единице.

Нулевым(или нуль-вектором) называется вектор 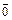, длина которого равна нулю.

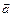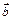Коллинеарными называются векторы и , если они лежат на одной прямой или на параллельных прямых; записывают .

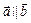Компланарными называются три вектораи более, если они лежат в одной плоскости или в параллельных плоскостях.

Равными ( 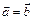)называются два коллинеарных вектора 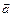и 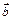, если они одинаково направлены и имеют равные длины.

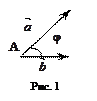Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор 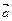имеет бесконечно много векторов, равных ему.

Углом между векторам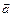и и 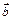называется наименьший угол 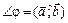, на который нужно повернуть вектор 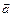, чтобы его направление совпало с направлением вектора 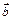, при условии, что оба вектора отнесены к общему началу, (рис.1).

Угол между векторами измеряется в пределах 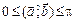. Если угол между векторами 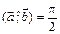(или 90°), то векторы называются ортогональными. В случае, когда 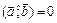(или 0°), говорят, что вектор 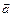сонаправлен с вектором 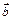, если же 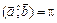(или 180°), то вектор 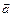имеет противоположное направление к вектору .

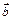Литература: [ 1, гл. 5, §5.1];[2, гл. 18, § 1, п. 5.6]; [ 3, гл. 2, п. 12.1];[4, гл. 2, § 5].

Координаты вектора и его длина

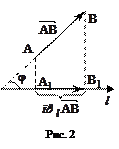
Пусть вектор 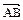составляет угол jс осью .

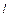Проекцией вектора 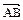на ось 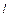называется число, равное длине вектора 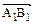(рис. 2), взятой со знаком плюс, если направление вектора 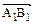совпадает с направлением оси 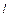, и со знаком минус в противном случае.

Проекция вектора 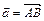на ось 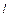вычисляется по формуле

.

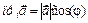Свойства проекций:

1. 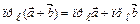; 2. .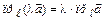

Декартовыми прямоугольными координатами 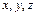вектора 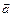называются его проекции на соответствующие координатные оси .

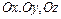Вектор 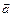с координатами 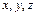записывают в координатной форме 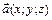или в виде разложения по базису 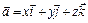, где 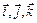–орты координатных осей 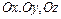соответственно (или базисные векторы).

Длина вектора 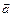определяется по формуле

.

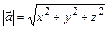Литература: [ 1, гл. 5, § 5.4];[2, гл. 18, § 7];[3, гл.2, п. 12.4];[4, гл. 2, § 5, п. 5.3].