Оценка достоверности результатов анализа

Поскольку результаты корреляционно-регрессионного анализа, полученные на базе ограниченного числа экспериментальных данных, являются случайными величинами, необходимо оценить их достоверность, определить доверительные интервалы, в которых находятся их истинные значения.

Для этого производится комплекс операций.

1. Оценка достоверности коэффициентов корреляции.

2. Оценка значимости коэффициентов регрессии.

3. Оценка адекватности уравнения регрессии.

Рассмотрим последовательность проведения операций.

1. При любом объеме выборки и многомерном нормальном распределении рассматриваемых факторов вычисляется статистика имеющая распределение Стьюдента с f=n-2 степенями свободы.

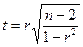, (16.1)

где r - коэффициент корреляции.

Для проверки нулевой гипотезы Н₀ (согласно которой коэффициент корреляции генеральной совокупности равен нулю) находят по таблицам, при фиксированном уровне значимости a и числе степеней свободы f=n-2, критическое значение 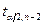, удовлетворяющее условию

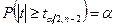
Если наблюдаемое значение 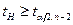, то нулевую гипотезу об отсутствии линейной зависимости между переменными x и y следует отвергнуть. Такой метод часто применяют при малом объеме выборок.

При числе наблюдений n>50 надежность коэффициента корреляции можно оценить по его среднему квадратическому отклонению

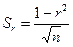(16.2)

и нормированному отклонению

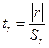(16.3)

Достоверность коэффициента корреляции считается доказанной с вероятностью 0,997, если t_r³3, с вероятностью 0,990 при t_r³2,58; с вероятностью 0,95 при t_r³1,96. Если n достаточно велико, а r близко к 0,5, то границы доверительного интервала для коэффициента корреляции генеральной совокупности r

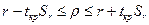(16.4)

Значение t_кр устанавливается по таблице функции Лапласа для выбранной вероятности. Если левая и правая части неравенства имеют одинаковый знак, то r имеет достоверный знак и является значимым.

Соотношения (16.1)-(16.4) справедливы и при оценке достоверности коэффициента множественной корреляции и корреляционных отношений.

2. Проверку значимости коэффициентов регрессии можно производить двумя способами: сравнением абсолютного значения коэффициента с доверительным интервалом и с помощью t-критерия Стьюдента.

В первом случае доверительный интервал для коэффициента b_i вычисляют по формуле

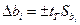
где t_T - табличное значение критерия Стьюдента при уровне значимости и числе степеней свободы, для которых определялось 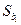, 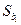- среднеквадратичное отклонение b_i. Коэффициент значим, если его абсолютное значение больше доверительно интервала.

При проверке значимости коэффициентов вторым способом вычисляют

,

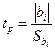и сравнивают его с критическим значением этого критерия t_кр. Коэффициент значим, если t_р>t_кр для принятого уровня значимости и числа степеней свободы, при которых определялось .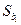

Методика определения 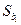зависит от способа получения уравнения регрессии. В случае применения планирования эксперимента:

,

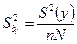где 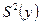- дисперсия воспроизводимости эксперимента, n- число параллельных опытов в каждой точке матрицы при равномерном дублировании опытов (при отсутствии дублирования n=1), N- общее число опытов в матрице плана.

При равномерном дублировании опытов во всех строках матрицы плана число параллельных опытов одинаково. Для каждой строки этой матрицы вычисляют дисперсию S_j результатов по данным n параллельных опытов

,

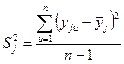где y_ju -значение функции отклика в j-й строке для u-ого опыта.

Если 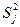результатов опытов однородны, то дисперсия 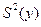воспроизводимости эксперимента

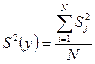, (16.5)

где N-число опытов или число строк матрицы плана.

При отсутствии дублирования опытов для определения дисперсии воспроизводимости эксперимента выполняют n₀ параллельных опытов при средних уровнях всех независимых факторов. По результатам этих опытов вычисляют

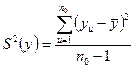, (16.6)

где y_u – значение функции отклика в u-ом параллельном опыте.

При равномерном дублировании опытов число степеней свободы для расчета 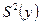и, следовательно 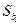находится как f=N(n-1), при отсутствии дублирования опытов f=n₀-1.

3. В зависимости о наличии сведений о дисперсии воспроизводимости эксперимента 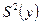проверку адекватности уравнения регрессии можно производить по двум схемам.

Схема I, состоящая из трех этапов применяется при отсутствии оценки дисперсии воспроизводимости, что характерно для пассивного эксперимента.

А) Вычисляется дисперсия относительно среднего значения параметра оптимизации:

.

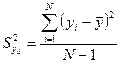Б) Рассчитывается дисперсия, характеризующая отклонение экспериментальных значений величин от найденных по уравнению регрессии. Если порядок уравнения заранее неизвестен, то в случае многофакторного пространства имеет смысл начинать с уравнения первого порядка.

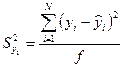, (16.7)

где 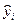- значение параметра оптимизации, вычисленное по уравнению регрессии для условий i-го опыта; f=N-g – число степеней свободы, g – число коэффициентов регрессии.

В) Вычисляется опытное значение отношения дисперсий

,

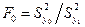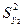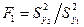которое затем сравнивают с критическим F_кр(f₁, f₂). Если F₀£F_кр, пользоваться уравнением регрессии первого порядка не имеет смысла, так как в изученном интервале изменения уровней факторов оно описывает исследуемую систему не лучше, чем уравнение нулевого порядка. Затем составляют уравнение второго порядка, рассчитывают и . Далее проверяют значимость этого отношения по критерию Фишера. Процедуру повторяют до тех пор, пока не будет выполнено условие F_r³F_кр(f_r,f_r+1).

Схема II применяется, если известна дисперсия воспроизводимости 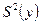эксперимента.

Для оценки адекватности модели, вначале рассчитывают дисперсию адекватности 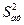по формуле (16.7), а затем вычисляют опытное значение критерия Фишера.

.

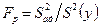Если F_p<F_кр(f_r,f_r+1), модель считают адекватной. Значение 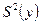определяют в зависимости от характера дублирования опытов по формулам (16.5) и (16.6).

Лекция №17